【题目】如图，在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 ， CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为（ ）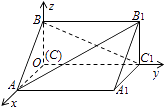
A.
B.
C.
D.
【答案】A
【解析】解：分别以CA、CC1、CB为x轴、y轴和z轴建立如图坐标系，
∵CA=CC1=2CB，∴可设CB=1，CA=CC1=2
∴A（2，0，0），B（0，0，1），B1（0，2，1），C1（0，2，0）
∴ 
=（0，2，﹣1）， 
=（﹣2，2，1）
可得 =0×（﹣2）+2×2+（﹣1）×1=3，且 
= 
， 
=3，
向量 与 所成的角（或其补角）就是直线BC1与直线AB1夹角，
设直线BC1与直线AB1夹角为θ，则cosθ=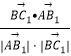 
= 
故选A
根据题意可设CB=1，CA=CC1=2，分别以CA、CC1、CB为x轴、y轴和z轴建立如图坐标系，得到A、B、B1、C1四个点的坐标，从而得到向量 与 的坐标，根据异面直线所成的角的定义，结合空间两个向量数量积的坐标公式，可以算出直线BC1与直线AB1夹角的余弦值．
科目：高中数学 来源： 题型：
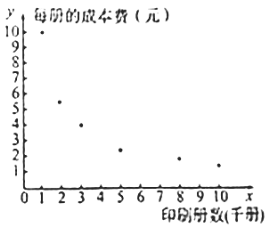
【题目】对某种书籍每册的成本费
（元）与印刷册数
（千册）的数据作了初步处理，得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
其中
，
.
为了预测印刷
千册时每册的成本费，建立了两个回归模型：
，
.
（1）根据散点图，你认为选择哪个模型预测更可靠？（只选出模型即可）
（2）根据所给数据和（1）中的模型选择，求关于
的回归方程，并预测印刷千册时每册的成本费.
附：对于一组数据
，
，…，
，其回归方程
的斜率和截距的最小二乘估计公式分别为：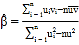
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点，已知AB=2，AD=2 
，PA=2，求： 
（1）三角形PCD的面积；
（2）异面直线BC与AE所成的角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
总决赛采用7场4胜制，2018年总决赛两支球队分别为勇士和骑士，假设每场比赛勇士获胜的概率为0.7，骑士获胜的概率为0.3，且每场比赛的结果相互独立，则恰好5场比赛决出总冠军的概率为__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设{an}是公比不为1的等比数列，其前n项和为Sn ， 且a5 ， a3 ， a4成等差数列．
（1）求数列{an}的公比；
（2）证明：对任意k∈N+ ， Sk+2 ， Sk ， Sk+1成等差数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了保护环境，某单位采用新工艺，把二氧化硅转化为一种可利用的化工产品.已知该单位每月都有处理量,且处理量最多不超过
吨，月处理成本
（元）与月处理量
（吨）之间的函数关系可近似的表示为：
，且每处理一吨二氧化硅得到可利用的化工产品价值为元.
（1）设该单位每月获利为
（元），试将表示月处理（吨）的函数；
（2）若要保证该单位每月不亏损，则每月处理量应控制在什么范围？
（3）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
