
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上为增函数,求
上为增函数,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的极值点,记作
有两个不同的极值点,记作![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() (
(![]() 为自然对数).
为自然对数).
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
分析:(1)由题意可知,函数![]() 的定义域为
的定义域为![]() ,
,![]() ,因为函数
,因为函数![]() 在
在![]() 为增函数,所以
为增函数,所以![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() ,
,
由此可求![]() 的取值范围;
的取值范围;
(2)求出![]() ,因为
,因为![]() 有两极值点
有两极值点![]() ,所以
,所以![]() ,
,
设令![]() ,则
,则![]() ,上式等价于要证
,上式等价于要证![]() ,令
,令![]() ,根据函数的单调性证出即可.
,根据函数的单调性证出即可.
详解:
(1)由题意可知,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
因为函数![]() 在
在![]() 为增函数,所以
为增函数,所以![]() 在
在![]() 上恒成立,
上恒成立,
等价于![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故![]() 的取值范围为
的取值范围为![]() .
.
(2)可知![]() ,
,
所以![]() ,
,
因为![]() 有两极值点
有两极值点![]() ,所以
,所以![]() ,
,
欲证![]() ,等价于要证:
,等价于要证:![]() ,即
,即![]() ,
,
所以![]() ,因为
,因为![]() ,所以原式等价于要证明:
,所以原式等价于要证明:![]() ,①
,①
由![]() ,可得
,可得![]() ,则有
,则有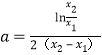 ,②
,②
由①②原式等价于要证明: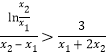 ,即证
,即证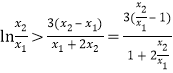 ,
,
令![]() ,则
,则![]() ,上式等价于要证
,上式等价于要证![]() ,
,
令![]() ,则
,则![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
因此当![]() 时,
时,![]() ,即
,即![]() .
.
所以原不等式成立,即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】小金同学在学校中贯彻着“边玩边学”的学风,他在“汉诺塔”的游戏中发现了数列递推的奥妙:有![]() 、
、![]() 、
、![]() 三个木桩,
三个木桩,![]() 木桩上套有编号分别为
木桩上套有编号分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到
的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到![]() 木桩上,则所需的最少次数为( )
木桩上,则所需的最少次数为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.

(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为[200,250),[250,300)的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知双曲线C1:2x2﹣y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ;
(3)设椭圆C2:4x2+y2=1,若M、N分别是C1、C2上的动点,且OM⊥ON,求证:O到直线MN的距离是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )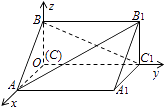
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知数列![]() 是等比数列,且公比为
是等比数列,且公比为![]() ,记
,记![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() =1,
=1,![]() >1,求
>1,求![]() 的值;
的值;
(2)若首项![]() ,
,![]() ,
,![]() 是正整数,满足不等式|
是正整数,满足不等式|![]() ﹣63|<62,且
﹣63|<62,且![]() 对于任意正整数
对于任意正整数![]() 都成立,问:这样的数列
都成立,问:这样的数列![]() 有几个?
有几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的两个顶点分别为
)的两个顶点分别为![]() 和
和![]() ,两个焦点分别为
,两个焦点分别为![]() 和
和![]() (
(![]() ),过点
),过点![]() 的直线
的直线![]() 与椭圆相交于另一点
与椭圆相交于另一点![]() ,且
,且![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设直线![]() 上有一点
上有一点![]() (
(![]() )在
)在![]() 的外接圆上,求
的外接圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若![]() q是
q是![]() p的必要不充分条件,求实数a的取值范围.
p的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com