
【题目】已知函数![]() .
.
(1)当![]() ,求
,求![]() 的最值;
的最值;
(2)若![]() 有两个不同的极值点,求
有两个不同的极值点,求![]() 的取值范围.
的取值范围.
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
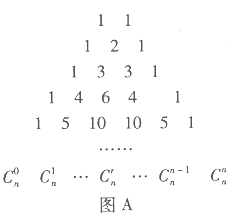
【题目】在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图![]() 所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”
所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”![]() ,如图
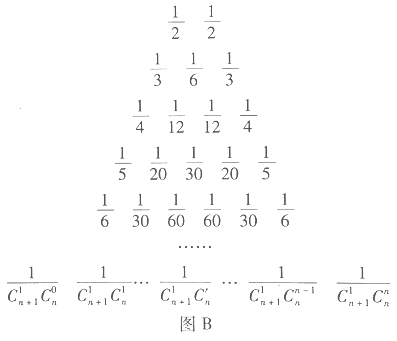
,如图![]() .17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图
.17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图![]() .在杨辉三角中,相邻两行满足关系式:
.在杨辉三角中,相邻两行满足关系式:![]() ,其 中
,其 中![]() 是行数,
是行数,![]() .请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
.请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2 ![]() ,PA=2,求:
,PA=2,求: 
(1)三角形PCD的面积;
(2)异面直线BC与AE所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比不为1的等比数列,其前n项和为Sn , 且a5 , a3 , a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N+ , Sk+2 , Sk , Sk+1成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护环境,某单位采用新工艺,把二氧化硅转化为一种可利用的化工产品.已知该单位每月都有处理量,且处理量最多不超过![]() 吨,月处理成本
吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:![]() ,且每处理一吨二氧化硅得到可利用的化工产品价值为
,且每处理一吨二氧化硅得到可利用的化工产品价值为![]() 元.
元.
(1)设该单位每月获利为![]() (元),试将
(元),试将![]() 表示月处理
表示月处理![]() (吨)的函数;
(吨)的函数;
(2)若要保证该单位每月不亏损,则每月处理量应控制在什么范围?
(3)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个结论:
①平行于同一直线的两条直线互相平行;
②垂直于同一平面的两个平面互相平行;
③若![]() ,
,![]() 是两个平面;
是两个平面;![]() ,
,![]() 是异面直线;且
是异面直线;且![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④若三棱锥![]() 中,
中,![]() ,
,![]() ,则点
,则点![]() 在平面
在平面![]() 内的射影是
内的射影是![]() 的垂心;
的垂心;
其中错误结论的序号为__________.(要求填上所有错误结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com