Question

【题目】如图，在三棱锥中，，，为的中点．

（1）证明：平面；

（2）若点在棱上，且，求点到平面的距离．

Answer 1

【答案】解：

（1）因为AP=CP=AC=4，O为AC的中点，所以OP⊥AC，且OP=．

连结OB．因为AB=BC=，所以△ABC为等腰直角三角形，且OB⊥AC，OB==2．

由知，OP⊥OB．

由OP⊥OB，OP⊥AC知PO⊥平面ABC．

（2）作CH⊥OM，垂足为H．又由（1）可得OP⊥CH，所以CH⊥平面POM．

故CH的长为点C到平面POM的距离．

由题设可知OC==2，CM==，∠ACB=45°．

所以OM=，CH==．

所以点C到平面POM的距离为．

【解析】分析：（1）连接，欲证平面，只需证明即可；（2）过点作，垂足为，只需论证的长即为所求，再利用平面几何知识求解即可.

详解：（1）因为AP=CP=AC=4，O为AC的中点，所以OP⊥AC，且OP=．

连结OB．因为AB=BC=，所以△ABC为等腰直角三角形，且OB⊥AC，OB==2．

由知，OP⊥OB．

由OP⊥OB，OP⊥AC知PO⊥平面ABC．

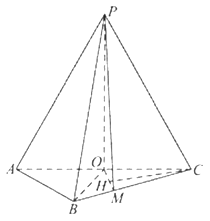
（2）作CH⊥OM，垂足为H．又由（1）可得OP⊥CH，所以CH⊥平面POM．

故CH的长为点C到平面POM的距离．

由题设可知OC==2，CM==，∠ACB=45°．

所以OM=，CH==．

所以点C到平面POM的距离为．