
【题目】已知数列{an}的前n项和为Sn , 且Sn+an=4,n∈N*
(1)求数列{an}的通项公式;
(2)已知cn=2n+3(n∈N*),记dn=cn+logCan(C>0,C≠1),是否存在这样的常数C,使得数列{dn}是常数列,若存在,求出C的值;若不存在,请说明理由.
(3)若数列{bn},对于任意的正整数n,均有 ![]() 成立,求证:数列{bn}是等差数列.
成立,求证:数列{bn}是等差数列.
【答案】
(1)解:∵Sn+an=4,n∈N*.∴当n≥2时,Sn﹣1+an﹣1=4,
∴an+an﹣an﹣1=0,即an= ![]() an﹣1.
an﹣1.
当n=1时,2a1=4,解得a1=2.
∴数列{an}是等比数列,an=2( ![]() )n﹣1=22﹣n
)n﹣1=22﹣n
(2)解:dn=cn+logCan=2n+3+logC22﹣n=2n+3+(2﹣n)logC2=(2﹣logC2)n+3+2logC2,
假设存在这样的常数C,使得数列{dn}是常数列,
则2﹣logC2=0,解得C= ![]() .
.
∴存在这样的常数C= ![]() ,使得数列{dn}是常数列,dn=3+2
,使得数列{dn}是常数列,dn=3+2 ![]() =7
=7
(3)解:证明:∵对于任意的正整数n,均有b1an+b2an﹣1+b3an﹣2+…+bna1=( ![]() )n﹣
)n﹣ ![]() 成立(*),
成立(*),
∴b1an+1+b2an+…+bna2+bn+1a1=( ![]() )n+1﹣
)n+1﹣ ![]() .①
.①
(*)两边同乘以 ![]() 可得:b1an+1+b2an+…+bna2=(
可得:b1an+1+b2an+…+bna2=( ![]() )n+1﹣
)n+1﹣ ![]() .②.
.②.
①﹣②可得bn+1a1= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴bn+1= ![]() ,
,
∴bn= ![]() ,(n≥3).
,(n≥3).
又2b1= ![]() ﹣
﹣ ![]() ,解得b1=﹣
,解得b1=﹣ ![]() .
.
b1a2+b2a1= ![]() ﹣
﹣ ![]() ,
,
∴﹣ ![]() ×1+b2×2=﹣
×1+b2×2=﹣ ![]() ,解得b2=﹣
,解得b2=﹣ ![]() .
.
当n=1,2时,bn= ![]() ,也适合.
,也适合.
∴bn= ![]() ,(n∈N*)是等差数列
,(n∈N*)是等差数列
【解析】(1)利用“当n=1时,a1=S1;当n≥2时,an=Sn﹣Sn﹣1”即可得出;(2)dn=cn+logCan=2n+3+logC22﹣n=(2﹣logC2)n+3+2logC2,假设存在这样的常数C,使得数列{dn}是常数列,则2﹣logC2=0,解得C即可;(3)由于对于任意的正整数n,均有b1an+b2an﹣1+b3an﹣2+…+bna1=( ![]() )n﹣
)n﹣ ![]() 成立(*),b1an+1+b2an+…+bna2+bn+1a1=(
成立(*),b1an+1+b2an+…+bna2+bn+1a1=( ![]() )n+1﹣
)n+1﹣ ![]() .(*)两边同乘以
.(*)两边同乘以 ![]() 可得:b1an+1+b2an+…+bna2=(
可得:b1an+1+b2an+…+bna2=( ![]() )n+1﹣
)n+1﹣ ![]() .两式相减可得可得bn+1=
.两式相减可得可得bn+1= ![]() ,即bn=
,即bn= ![]() ,(n≥3).n=1,2也成立,即可证明.
,(n≥3).n=1,2也成立,即可证明.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系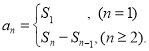 .
.


科目:高中数学 来源: 题型:
【题目】已知动圆![]() 恒过点
恒过点![]() ,且与直线
,且与直线![]() :
: ![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)探究在曲线![]() 上,是否存在异于原点的两点
上,是否存在异于原点的两点![]() ,
, ![]() ,当
,当![]() 时,直线
时,直线![]() 恒过定点?若存在,求出该定点坐标;若不存在,请说明理由.
恒过定点?若存在,求出该定点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=![]() ,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的命题个数是 ( )
①. 如果![]() 共面,
共面, ![]() 也共面,则
也共面,则![]() 共面;
共面;
②.已知直线a的方向向量![]() 与平面
与平面![]() ,若
,若![]() //
// ![]() ,则直线a//
,则直线a// ![]() ;
;
③若![]() 共面,则存在唯一实数
共面,则存在唯一实数![]() 使
使![]() ,反之也成立;
,反之也成立;
④.对空间任意点O与不共线的三点A、B、C,若![]() =x
=x![]() +y
+y![]() +z
+z![]()
(其中x、y、z∈R),则P、A、B、C四点共面
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() +2﹣2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
+2﹣2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
(1)求a,b满足的关系式;
(2)若f(x)≥2lnx在[1,+∞)上恒成立,求a的取值范围;
(3)证明:1+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() (2n+1)+
(2n+1)+ ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com