
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() .
.
(1)若抛物线![]() 和直线
和直线![]() 没有公共点,求
没有公共点,求![]() 的取值范围;
的取值范围;
(2)若![]() ,且抛物线
,且抛物线![]() 和直线
和直线![]() 只有一个公共点
只有一个公共点![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() 或
或![]() ;(2)2.
;(2)2.
【解析】试题分析:(1)联立方程![]() ,整理得
,整理得![]() ,
,
由抛物线![]() 和直线
和直线![]() 没有公共点,则
没有公共点,则![]() ,即可求得k的取值范围;
,即可求得k的取值范围;
(2)当抛物线![]() 和直线
和直线![]() 只有一个公共点时,记公共点坐标为
只有一个公共点时,记公共点坐标为![]() ,由
,由![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,因为
,因为![]() ,故
,故![]() ,将
,将![]() 代入
代入![]() 得
得![]() 求得x的值即得点M的坐标,可求
求得x的值即得点M的坐标,可求![]() 的值.
的值.
试题解析:(1)联立方程![]() ,
,
整理得![]() ,
,
由抛物线![]() 和直线
和直线![]() 没有公共点,则
没有公共点,则![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() .
.
(2)当抛物线![]() 和直线
和直线![]() 只有一个公共点时,记公共点坐标为
只有一个公共点时,记公共点坐标为![]() ,
,
由![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
因为![]() ,故
,故![]() ,
,
将![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,
由抛物线的定义知:![]() .
.
点睛:抛物线的定义是解决抛物线问题的基础,它能将两种距离(抛物线上的点到焦点的距离、抛物线上的点到准线的距离)进行等量转化.如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么用抛物线定义就能解决问题.因此,涉及抛物线的焦半径、焦点弦问题,可以优先考虑利用抛物线的定义转化为点到准线的距离,这样就可以使问题简单化.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() ,g(x)=x2﹣2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),求实数a的取值范围.
,g(x)=x2﹣2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.设向量 ![]() =(a,c),
=(a,c), ![]() =(cosC,cosA).
=(cosC,cosA).
(1)若 ![]() ,c=
,c= ![]() a,求角A;
a,求角A;
(2)若 ![]() =3bsinB,cosA=
=3bsinB,cosA= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
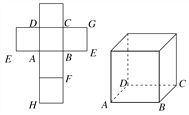
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,﹣2),椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为 ![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)求E的方程;
(Ⅱ)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2009年广东卷文)某单位200名职工的年龄分布情况如图2,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是 。若用分层抽样方法,则40岁以下年龄段应抽取 人.

图 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1g(1﹣x)的值域为(﹣∞,0),则函数f(x)的定义域为( )
A.[0,+∞]
B.(0,1)
C.[﹣9,+∞)
D.[﹣9,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn+an=4,n∈N*
(1)求数列{an}的通项公式;
(2)已知cn=2n+3(n∈N*),记dn=cn+logCan(C>0,C≠1),是否存在这样的常数C,使得数列{dn}是常数列,若存在,求出C的值;若不存在,请说明理由.
(3)若数列{bn},对于任意的正整数n,均有 ![]() 成立,求证:数列{bn}是等差数列.
成立,求证:数列{bn}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米. 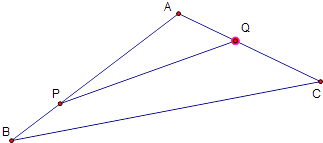
(1)当x,y为何值时?游客体验活动区APQ的面积最大,并求最大面积;
(2)当x,y为何值时?线段|PQ|最小,并求最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com