
【题目】已知首项都是1的两个数列{![]() },{
},{![]() }(
}(![]() ≠0,n∈N*)满足
≠0,n∈N*)满足![]()
(1)令![]() ,求数列{
,求数列{![]() }的通项公式;
}的通项公式;
(2)若![]() =
=![]() ,求数列{
,求数列{![]() }的前n项和
}的前n项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)![]() 两边同时除以
两边同时除以![]() ,得
,得![]() ,可得
,可得![]() .
.
(2)由(1)![]() ,所以
,所以![]() ,由错位相减法可求和。
,由错位相减法可求和。
(1)因为anbn+1-an+1bn+2bn+1bn=0,bn≠0(n∈N*),所以![]() ,即cn+1-cn=2,
,即cn+1-cn=2,
所以数列{cn}是以c1=1为首项,d=2为公差的等差数列,故cn=2n-1.
(2)由bn=3n-1,知an=(2n-1)3n-1,于是数列{an}的前n项和
Sn=1×30+3×31+5×32+…+(2n-1)×3n-1,
3Sn=1×31+3×32+…+(2n-3)×3n-1+(2n-1)×3n,
将两式相减得-2Sn=1+2×(31+32+…+3n-1)-(2n-1)×3n=-2-(2n-2)×3n,
所以Sn=(n-1)3n+1.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.设向量 ![]() =(a,c),
=(a,c), ![]() =(cosC,cosA).
=(cosC,cosA).
(1)若 ![]() ,c=
,c= ![]() a,求角A;
a,求角A;
(2)若 ![]() =3bsinB,cosA=
=3bsinB,cosA= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1g(1﹣x)的值域为(﹣∞,0),则函数f(x)的定义域为( )
A.[0,+∞]
B.(0,1)
C.[﹣9,+∞)
D.[﹣9,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn+an=4,n∈N*
(1)求数列{an}的通项公式;
(2)已知cn=2n+3(n∈N*),记dn=cn+logCan(C>0,C≠1),是否存在这样的常数C,使得数列{dn}是常数列,若存在,求出C的值;若不存在,请说明理由.
(3)若数列{bn},对于任意的正整数n,均有 ![]() 成立,求证:数列{bn}是等差数列.
成立,求证:数列{bn}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
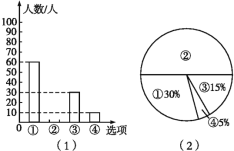
(1)本次一共调查了多少名学生.(2)在图(1)中将②对应的部分补充完整.
(3)若该校有3 000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5时以下?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元,该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元,假设商店每月购进这种商品m件,且当月销完,你估计哪个月份盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米. 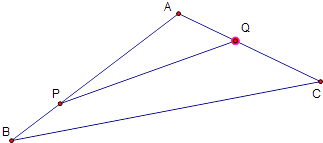
(1)当x,y为何值时?游客体验活动区APQ的面积最大,并求最大面积;
(2)当x,y为何值时?线段|PQ|最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输队接到给灾区运送物资的任务,该运输队有8辆载重为![]() 的
的![]() 型卡车,6辆载重为
型卡车,6辆载重为![]() 的
的![]() 型卡车,10名驾驶员,要求此运输队每天至少运送
型卡车,10名驾驶员,要求此运输队每天至少运送![]() 救灾物资.已知每辆卡车每天往返的次数为
救灾物资.已知每辆卡车每天往返的次数为![]() 型卡车16次,
型卡车16次, ![]() 型卡车12次.每辆卡车每天往返的成本为
型卡车12次.每辆卡车每天往返的成本为![]() 型卡车240元,
型卡车240元, ![]() 型卡车378元.问每天派出
型卡车378元.问每天派出![]() 型卡车与
型卡车与![]() 型卡车各多少辆,运输队所花的成本最低?
型卡车各多少辆,运输队所花的成本最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com