【题目】(2015·江苏）在△ABC中，已知AB=2，AC=3，A=60°.
（1）求BC的长；
（2）求sin2C的值.
【答案】
（1）
（2）
【解析】已知两边及夹角求第三边，应用余弦定理，可得BC的长，(2) 用(1)的结果，则内余弦定理先求出角C的余弦值，再根据平方关系及三角形角的范围求出角C的正弦值，最后利用二倍角公式求出sin2C的值.
由余弦定理知，BC2=AB2+AC2-2AB·AC·cosA=4+9-2x2x3x
=7, 所以BC=。
由正弦定理， 
,所以sinC=
·sinA=
=
.
因为AB<BC, 所以C为锐角，则cosC=
=
=
, 因此sin2C=2sinCcosC=2xx=.
【考点精析】解答此题的关键在于理解二倍角的正弦公式的相关知识，掌握二倍角的正弦公式：
，以及对余弦定理的定义的理解，了解余弦定理:
;
;
．
黄冈天天练口算题卡系列答案科目：高中数学 来源： 题型：
【题目】
已知椭圆C：
+
=1,(a
b0)的离心率为
，点（2，
）在C上
（1）求C的方程；
（2）直线l不经过原点O,且不平行于坐标轴,l与C有两个交点A,B,线段AB中点为M,证明：直线OM的斜率与直线l的斜率乘积为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2015·四川）已知A、B、C为△ABC的内角，tanA、tanB是关于方程x2＋
px－p＋1＝0(p∈R)两个实根.
（1）求C的大小
（2）若AB＝1，AC＝
，求p的值
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2015·陕西）如图，椭圆E:
(a>b>0)经过点A(0,-1)，且离心率为
.
（1）求椭圆E的方程；
（2）经过点(1,1)，且斜率为k的直线与椭圆E交于不同两点P,Q（均异于点A），证明：直线AP与AQ的斜率之和为2.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2015·陕西）设fn(x)=x+x2+x...+xn-1, n
N, n≥2。
（1）fn'(2)
（2）证明:fn(x)在（0，
）内有且仅有一个零点（记为an)， 且0<an-
<
()n.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2015·江苏） 已知函数f(x)=x3+ax2+b(a,b
R).
（1）试讨论f(x)的单调性；
（2）若b=c-a（实数c是a与无关的常数），当函数f(x)有三个不同的零点时，a的取值范围恰好是(-
,-3)
(1,
)(,+)，求c的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2015·湖南）已知抛物线C1：x2=4y的焦点F也是椭圆C2:
(a>b>0)的一个焦点，C1与C2的公共弦长为2
，过点F的直线l与C1相交于A, B两点，与C2相交于C,D两点，且
与
同向.
（1）求C2的方程
（2）若|AC|=|BD|，求直线l的斜率
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
某电子商务公司对10000名网络购物者2014年度的消费情况进行统计，发现消费金额
（单位：万元）都在区间
内，其频率分布直方图如图所示.
（Ⅰ）直方图中的
；
（Ⅱ）在这些购物者中，消费金额在区间
内的购物者的人数为 .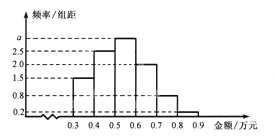 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
