
分析 (I)运用离心率公式和a,b,c的关系,以及两点的距离公式,解方程可得椭圆方程;
(II)设A(x1,y1),B(x2,y2),将y=kx+2代入椭圆,可得x的方程,运用韦达定理和判别式大于0,求得三角形的面积,化简整理,运用基本不等式即可得到所求最大值.
解答 解:(I)由已知得$\frac{c^2}{a^2}=\frac{1}{3}$,又由a2=b2+c2,
可得a2=3c2,b2=2c2,
得椭圆方程为$\frac{x^2}{{3{c^2}}}+\frac{y^2}{{2{c^2}}}=1$,
因为点M在第一象限且MF2⊥x轴,
可得M的坐标为$({c,\frac{{2\sqrt{3}}}{3}c})$,
由$|{{F_1}M}|=\sqrt{4{c^2}+\frac{4}{3}{c^2}}=\frac{{4\sqrt{3}}}{3}$,解得c=1,
所以椭圆方程为$\frac{x^2}{3}+\frac{y^2}{2}=1$;
(II)设A(x1,y1),B(x2,y2),
将y=kx+2代入椭圆,可得(3k2+2)x2+12kx+6=0,
由△>0,即144k2-24(3k2+2)>0,可得3k2-2>0,
则有${x_1}+{x_2}=-\frac{12k}{{2+3{k^2}}},{x_1}{x_2}=\frac{6}{{2+3{k^2}}}$
所以$|{{x_1}-{x_2}}|=\frac{{2\sqrt{18{k^2}-12}}}{{3{k^2}+2}}$,
因为直线y=kx+2与轴交点的坐标为(0,2),
所以△OAB的面积$S=\frac{1}{2}×2×|{{x_1}-{x_2}}|=\frac{{2\sqrt{(18{k^2}-12)}}}{{3{k^2}+2}}=\frac{{2\sqrt{6×(3{k^2}-2)}}}{{3{k^2}+2}}$,
令3k2-2=t,由①知t∈(0,+∞),
可得$S=2\frac{{\sqrt{6t}}}{t+4}=2\sqrt{\frac{6t}{{{t^2}+8t+16}}}=2\sqrt{\frac{6}{{t+\frac{16}{t}+8}}}≤\frac{{\sqrt{6}}}{2}$,
所以t=4时,面积最大为$\frac{{\sqrt{6}}}{2}$.
点评 本题考查椭圆方程的求法,注意运用离心率公式,考查三角形的面积的最值的求法,注意运用直线方程和椭圆方程联立,运用韦达定理和弦长公式,以及基本不等式,考查化简整理的运算能力,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5 | C. | 10 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
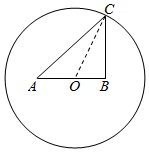 某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏.
某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{3}{7}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) | B. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{5}$=1(x≠0) | C. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(x≠3) | D. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{5}$=1(y≠3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com