
 ij������һԲ��ˮ�������������۾���Ȫ���۾���Ȫ��ʾ��ͼ��ͼ��ʾ��A��B����Ϊ��Ȫ��Բ��OΪAB���е㣬����OA=OB=a�ף��뾶OC=10�ף������λ��ˮ�ر�Ե����һ��C�����ͣ�
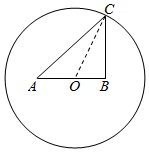
ij������һԲ��ˮ�������������۾���Ȫ���۾���Ȫ��ʾ��ͼ��ͼ��ʾ��A��B����Ϊ��Ȫ��Բ��OΪAB���е㣬����OA=OB=a�ף��뾶OC=10�ף������λ��ˮ�ر�Ե����һ��C�����ͣ����� ��1������OBC=$\frac{2��}{3}$ʱ��sin��BCO=$\frac{1}{3}$�������Ҷ������ʱa��ֵ��
��2����i���������Ҷ��������CA2+CB2��232����200+2a2��232���ɽ�y��ʾΪa�ĺ����������a��ȡֵ��Χ��
��ii�������ͽǶȡ�ACB�����ʱ��cos��ACBȡ����Сֵ�������Ҷ����ɵý��ۣ�
��� �⣺��1���ڡ�OBC�У������Ҷ����ã�$\frac{OC}{sin��OBC}=\frac{OB}{sin��BCO}$��
��$OB=a=\frac{{20\sqrt{3}}}{9}$������3�֣�
��2����i����֪AC2=100+a2-20acos��AOC��BC2=100+a2-20acos��BOC��
��CA2+CB2=200+2a2������5�֣�
����ΪCA2+CB2��232����200+2a2��232�����0��a��4��
��y=200+2a2��a�ʣ�0��4]������7�֣�
��ii�������ͽǶȡ�ACB�����ʱ��cos��ACBȡ����Сֵ�������Ҷ����ɵ�$cos��ACB=\frac{{C{A^2}+C{B^2}-4{a^2}}}{2CA•CB}��\frac{{C{A^2}+C{B^2}-4{a^2}}}{{C{A^2}+C{B^2}}}=1-\frac{{2{a^2}}}{{100+{a^2}}}$��
��$cos��ACB��1-\frac{{2{a^2}}}{{100+{a^2}}}$����11�֣�
�������֪$1-\frac{{2{a^2}}}{{100+{a^2}}}��\frac{{\sqrt{3}}}{2}$����˲���ʽ��$a��20-10\sqrt{3}$��
����֤��$20-10\sqrt{3}�ʣ�0��4]$����$2a��40-20\sqrt{3}$������13�֣�
�𣺣�1����ʱ$a=\frac{{20\sqrt{3}}}{9}$��
��2����i�����ú�����ϵʽΪy=200+2a2��a�ʣ�0��4]��
��ii��A��B������Ȫ��������СֵΪ$40-20\sqrt{3}$������14�֣�
���� ���⿼���������֪ʶ�����ã��������Ҷ���������ѧ�������������������������е��⣮


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
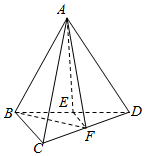 ���磬������A-BCD�У�AB=AD��BC��CD��ƽ��ABD��ƽ��BCD����E��F�ֱ���BD��CD���е㣮
���磬������A-BCD�У�AB=AD��BC��CD��ƽ��ABD��ƽ��BCD����E��F�ֱ���BD��CD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 3 | C�� | 0 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com