
分析 (1),(2)根据指数函数的性质求出a的范围即可;(3)通过讨论p,q的真假,求出a的范围即可.
解答 解:(1)命题p:“函数f(x)=(a-$\frac{3}{2}$)x是R上的减函数”为真命题,
得0<a-$\frac{3}{2}$<1,∴$\frac{3}{2}$<a<$\frac{5}{2}$;
(2)由q为真命题,则由0<$(\frac{1}{2})$|x-1|≤1,得a>1;
(3)∵p且q为假,p或q为真,∴p、q中一真一假,
若p真q假,则a不存在;
若p假q真,则1<a≤$\frac{3}{2}$或a≥$\frac{5}{2}$;
综上,a的取值范围为:1<a≤$\frac{3}{2}$或a≥$\frac{5}{2}$.
点评 本题考查了指数函数的性质,考查复合命题的判断,是一道基础题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
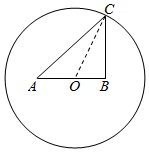 某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏.
某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+(y-2)2=5 | B. | (x-2)2+(y-1)2=5 | C. | (x-1)2+(y+2)2=5 | D. | (x-2)2+(y+1)2=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) | B. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{5}$=1(x≠0) | C. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(x≠3) | D. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{5}$=1(y≠3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com