
分析 解化简复数,结合复数实部和虚部的关系建立方程即可得到结论.
解答 解:z=$\frac{a+i}{2i}$=$\frac{ai+{i}^{2}}{2{i}^{2}}$=$\frac{-1+ai}{-2}$=$\frac{1}{2}$-$\frac{a}{2}$i,
∵复数的实部与虚部相等,
∴$\frac{1}{2}$=-$\frac{a}{2}$,即a=-1,则z=$\frac{1}{2}$+$\frac{1}{2}$i,
则|z|=$\sqrt{(\frac{1}{2})^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查复数的模长的计算,根据复数的四则运算进行化简是解决本题的关键,比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
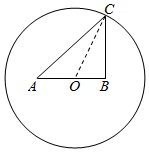 某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏.
某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+(y-2)2=5 | B. | (x-2)2+(y-1)2=5 | C. | (x-1)2+(y+2)2=5 | D. | (x-2)2+(y+1)2=5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com