
分析 (1)由题意可得a=2b,b=1,解得a=2,进而得到椭圆方程;
(2)设P(x1,y1),Q(x2,y2),联立直线l的方程和椭圆方程,运用韦达定理,可得Q的坐标,由点B在以PQ为直径圆内,得∠PBQ为钝角或平角,即有$\overrightarrow{BP}•\overrightarrow{BQ}<0$,运用数量积的坐标表示,解不等式即可得到所求范围.
解答 解:(1)由题意知,a=2b,b=1,解得a=2,
可得椭圆的标准方程为:$\frac{x^2}{4}+{y^2}=1$;
(2)设P(x1,y1),Q(x2,y2)
联立$\left\{\begin{array}{l}y=k(x+2)\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$,消去y,得(1+4k2)x2+16k2x+16k2-4=0,(*)
依题意:直线l:y=k(x+2)恒过点(-2,0),
此点为椭圆的左顶点,所以x1=-2,y1=0 ①,
由(*)式,${x_1}+{x_2}=-\frac{{16{k^2}}}{{1+4{k^2}}}$ ②,
得y1+y2=k(x1+x2)+4k③,
由①②③,可得${x_2}=\frac{{2-8{k^2}}}{{1+4{k^2}}},\;{y_2}=\frac{4k}{{1+4{k^2}}}$,
由点B在以PQ为直径圆内,得∠PBQ为钝角或平角,
即$\overrightarrow{BP}•\overrightarrow{BQ}<0$.$\overrightarrow{BP}=(-2,\;1),\;\overrightarrow{BQ}=({x_2},\;{y_2}-1)$
$\overrightarrow{BP}•\overrightarrow{BQ}=-2{x_2}-{y_2}+1<0$.即$\frac{{4-16{k^2}}}{{1+4{k^2}}}+\frac{4k}{{1+4{k^2}}}-1>0$,
整理得20k2-4k-3<0,解得$k∈({-\frac{3}{10},\;\frac{1}{2}})$.
点评 本题考查椭圆方程的求法,注意运用椭圆的性质,考查实数的取值范围,注意联立直线方程和椭圆方程,运用韦达定理,考查点在圆内的条件:点与直径的端点的张角为钝角或平角,运用数量积小于0,考查化简整理的运算能力,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | -$\frac{6}{7}$ | C. | $\frac{21}{16}$ | D. | $\frac{22}{31}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
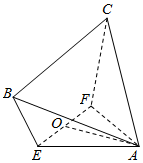 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{17}{8}$ | C. | $\frac{{3\sqrt{3}-1}}{2}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com