Question

【题目】设a,b,c分别是的三条边,且.我们知道,如果为直角三角形,那么(勾股定理).反过来,如果,那么为直角三角形(勾股定理的逆定理).由此可知,为直角三角形的充要条件是.请利用边长a,b,c分别给出为锐角三角形和钝角三角形的一个充要条件,并证明.

Answer 1

【答案】为锐角三角形的充要条件是.为钝角三角形的充要条件是.证明见解析

【解析】

根据勾股定理易得为锐角三角形的充要条件是.为钝角三角形的充要条件是.再分别证明充分与必要性即可.

解:(1)设a,b,c分别是的三条边,且,为锐角三角形的充要条件是.

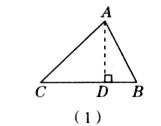
证明如下:必要性:在中,是锐角,作,D为垂足,如图(1).

显然

,即.

充分性:在中,,不是直角.

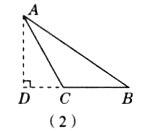
假设为钝角,如图(2).作,交BC延长线于点D.

则

.

即,与“”矛盾.

故为锐角,即为锐角三角形.

(2)设a,b,c分别是的三条边,且,为钝角三角形的充要条件是.

证明如下:必要性:在中,为钝角,如图(2),显然:

.即.

充分性:在中,,

不是直角,假设为锐角,如图(1),

则

.即,这与“”矛盾,从而必为钝角,即为钝角三角形.