
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点.将△
的中点.将△![]() 沿
沿![]() 翻折,得到四棱锥
翻折,得到四棱锥![]() .设线段
.设线段![]() 的中点为
的中点为![]() ,在翻折过程中,有下列三个命题:
,在翻折过程中,有下列三个命题:
① 总有![]() 平面
平面![]() ;
;
② 三棱锥![]() 体积的最大值为
体积的最大值为![]() ;
;
③ 存在某个位置,使![]() 与
与![]() 所成的角为
所成的角为![]() .
.
其中正确的命题是____.(写出所有正确命题的序号)

科目:高中数学 来源: 题型:
【题目】如图(1),平面直角坐标系中,![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() ,两圆内切于点
,两圆内切于点![]() ,动圆
,动圆![]() 与
与![]() 外切,与
外切,与![]() 内切.
内切.

(1)求动圆![]() 圆心
圆心![]() 的轨迹方程;
的轨迹方程;
(2)如图(2),过![]() 点作
点作![]() 的两条切线
的两条切线![]() ,若圆心在直线
,若圆心在直线![]() 上的
上的![]() 也同时与
也同时与![]() 相切,则称
相切,则称![]() 为
为![]() 的一个“反演圆”
的一个“反演圆”

(ⅰ)当![]() 时,求证:
时,求证:![]() 的半径为定值;
的半径为定值;
(ⅱ)在(ⅰ)的条件下,已知![]() 均与
均与![]() 外切,与
外切,与![]() 内切,且
内切,且![]() 的圆心为
的圆心为![]() ,求证:若
,求证:若![]() 的“反演圆”
的“反演圆”![]() 相切,则
相切,则![]() 也相切。
也相切。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三有500名学生,在一次考试的英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
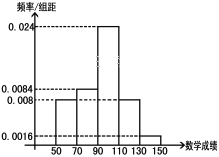
(Ⅰ)如果成绩大于135的为特别优秀,则本次考试英语、数学特别优秀的大约各多少人?
(Ⅱ)试问本次考试英语和数学的成绩哪个较高,并说明理由.
(Ⅲ)如果英语和数学两科都特别优秀的共有6人,从(Ⅰ)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望。
的分布列和数学期望。
参考公式及数据:
若![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国青年报》2015年5月14日报道:“伴随着网络技术的蓬勃发展,国内电子商务获得了爆炸式的增长,2014年网上零售额达到了27898亿元,占社会消费品零售总额的10%,也就是说,人们日常消费中10%是通过网购,而且还以年30%,40%的速度增长."假设2014-2020年网上零售额每年的增长率均为35%,试算出2015-2020年每年的网上零售额(精确到1亿元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在促销期间规定:商场内所有商品按标价的![]() 出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围 |
|
|
|
| … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为:![]() 元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,顾客购买标价为多少元的商品,可得到不小于
(元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 与
与![]() 轴、
轴、![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() ,
,![]() 两点.
两点.
(1)求线段![]() 中点
中点![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)若![]() 是(1)中点
是(1)中点![]() 的轨迹上的动点,求
的轨迹上的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b,c分别是![]() 的三条边,且
的三条边,且![]() .我们知道,如果
.我们知道,如果![]() 为直角三角形,那么
为直角三角形,那么![]() (勾股定理).反过来,如果
(勾股定理).反过来,如果![]() ,那么
,那么![]() 为直角三角形(勾股定理的逆定理).由此可知,
为直角三角形(勾股定理的逆定理).由此可知,![]() 为直角三角形的充要条件是
为直角三角形的充要条件是![]() .请利用边长a,b,c分别给出
.请利用边长a,b,c分别给出![]() 为锐角三角形和钝角三角形的一个充要条件,并证明.
为锐角三角形和钝角三角形的一个充要条件,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com