解:(1)∵函数f(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称;(2分)
又∵
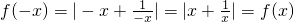
,∴f(x)是偶函数.(4分)
(2)证明:当x∈(0,+∞)时,

,
则
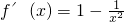
易得当x∈(0,1)时,f′(x)<0,当x∈(1,+∞)时,f′(x)>0
故函数f(x)在(0,1)上是单调减函数,在[1,+∞)上是单调增函数;
(3)函数f(x)图象如图所示(14分)
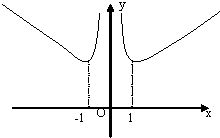
函数f(x)的单调增区间是[-1,0),[1,+∞),
单调减区间是(-∞,-1],(0,1],值域是[2,+∞)(16分)
分析:(1)分析函数的定义域是否关于原点对称,及f(-x)与f(x)的关系,然后根据函数奇偶性的定义即可得到答案.
(2)根据已知中函数的解析式,我们可以求出x∈(0,+∞)时,函数的解析式及导函数的解析式,然后根据x∈(0,1)时与x∈(1,+∞)时,f′(x)的符号,即可得到结论;
(3)由(1)(2)的结论,结合描点法,我们易得到函数的图象,根据图象易求出函数f(x)的单调区间及值域.
点评:本题考查的知识点是函数奇偶性的判断及函数单调性的判断与证明,函数图象的画法及应用,属于函数的综合性应用问题,考查了函数除了周期性以外的所有重要知识点,是一道不可多得的好题.

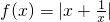
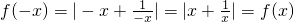 ,∴f(x)是偶函数.(4分)
,∴f(x)是偶函数.(4分) ,
,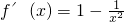



 已知函数函f(x)=x|x|-2x (x∈R)
已知函数函f(x)=x|x|-2x (x∈R)
 ,
, ,
, ,
, 这几个函数值,你能发现f(x)与
这几个函数值,你能发现f(x)与 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;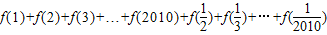 的值;
的值; 在区间(0,+∞)上的单调性.
在区间(0,+∞)上的单调性.