f(x)=-2x2+mx-3在(-∞.3]上是增函数.则实数m的取值范围是( )A．{1.2}B．[6.+∞)C．[12.+∞)D．(-∞.6] 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

18．f（x）=-2x²+mx-3在（-∞，3]上是增函数，则实数m的取值范围是（　　）

A．

{1，2}

B．

[6，+∞）

C．

[12，+∞）

D．

（-∞，6]

分析先求出函数的对称轴，再由题意和二次函数的单调性列出不等式，求出m的范围即可．

解答解：函数f（x）=-2x²+mx-3的对称轴是x=$\frac{m}{4}$，
∵函数在（-∞，3]）上是增函数，
∴$\frac{m}{4}$≥3，解得m≥12，
故选：C．

点评本题考查了二次函数的单调性与对称轴的应用，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

8．

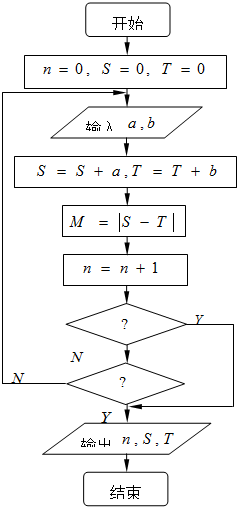在某次中国象棋比赛中，组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T．比赛约定每局胜者得1分，负者得0分，平局不作统计．如果一方获胜，输入a=1，b=0，另一方获胜，则输入a=0，b=1，比赛进行满6局或一方分数高于对方2分者即结束，则图中第一、第二两个判断框分别填写的条件错误的是（　　）

A．

M≥2，n＞5

B．

M=2，n=6

C．

M＞1，n≥6

D．

M≥2，n＜7

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．已知函数y=f（x+1）定义域是[-2，1]，则y=f（2x-1）的定义域（　　）

A．

[0，$\frac{3}{2}$]

B．

[-1，4]

C．

[-5，5]

D．

[-3，7]

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．设各项为正数的数列{a_n}的前n和为S_n，且S_n满足：${S_n}^2-（{n^2}+n-3）{S_n}-3（{n^2}+n）=0，n∈{N_+}$．等比数列{b_n}满足：${log_2}{b_n}+\frac{1}{2}{a_n}=0$．
（Ⅰ）求数列{a_n}，{b_n}的通项公式；
（Ⅱ）设c_n=a_n•b_n，求数列{c_n}的前n项的和T_n；
（Ⅲ）证明：对一切正整数n，有$\frac{1}{{{a_1}（{a_1}+1）}}+\frac{1}{{{a_2}（{a_2}+1）}}+…+\frac{1}{{{a_n}（{a_n}+1）}}＜\frac{1}{3}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．两平行直线2x+3y-8=0与2x+3y+18=0之间的距离d=2$\sqrt{13}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

3．已知A∪B∪C={a，b，c，d，e}，A∩B={a，b，c}，c∈A∩B∩C，则符合上述条件的{A，B，C}共有100组．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

10．若$\frac{1}{a}$＜$\frac{1}{b}$＜0，则下列结论不正确的是（　　）

A．

a²＜b²

B．