
如图长度为2的线段AB夹在直二面角![]() 的两个半面内,
的两个半面内,![]() ,且AB与平面
,且AB与平面![]() 所成的角都是30°,AC⊥l,垂足为C,BD⊥l,垂足为D。
所成的角都是30°,AC⊥l,垂足为C,BD⊥l,垂足为D。
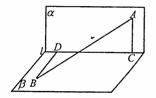
(1)求直线AB与CD所成角的大小;
(2)求二面角C―AB―D的平面角的余弦值。
解法一:
(1)由于![]() 且AC⊥l,则AC⊥
且AC⊥l,则AC⊥![]() ,以C为原点,建立如图所示的直角坐标系。
,以C为原点,建立如图所示的直角坐标系。

因为AB=2,AB与平面![]() 所成的角都是30°,且AC⊥l于C,BD⊥l于D,则AC=1,BD=1。AD=
所成的角都是30°,且AC⊥l于C,BD⊥l于D,则AC=1,BD=1。AD=![]() ,所以A(0,0,1)、M(1,-
,所以A(0,0,1)、M(1,-![]() ,0)、C(0,0,0)、
,0)、C(0,0,0)、
D(0,-![]() ,0)(2分)
,0)(2分)![]()

故直线AB与CD所成角为45°。
(2)设平面ABC的一个法向量![]()
由
取![]()
设平面ABE的一个法向量为![]()
由

取![]()
由![]()
故二面角C―AB―D的平面角的余弦值为![]()
解法二:
(1)在平面![]() 内过点B作BE//DC,BE=DC,连结CE,EA,BC,AD,
内过点B作BE//DC,BE=DC,连结CE,EA,BC,AD,
则四边形BECD是矩形。

所以∠ABE就是直线AB与CD所成角。
∵AB=2,![]() ⊥
⊥![]() ,AC⊥l,AC
,AC⊥l,AC![]()
![]()
∴AC⊥![]()
∴∠ABC=30°。
∴AC=1,同理BD=1。
∴CE=1,AE=![]()
∵CE⊥BE,
∴AE⊥BE。
在Rt△AEB中,sin∠ABE=![]()
∴∠ABC=45°.
∴直线AB与CD所成角的大小为45°
(2)∵AC⊥![]() ,AC
,AC![]() 平面ABC。
平面ABC。
∴平面BAC⊥平面BDC,且交线是BC,
过点D作DF⊥BC,垂足为F,则DF⊥平面BAC,
过F作FG⊥AB,垂足为G,连结DG,则DG⊥AB,
故∠DGF就是二面角C―AB―D的平面角。
在Rt △ACB中,BC=![]()
在Rt △BDC中,DC=![]()
![]()
在Rt△BGF中,FG=BF![]()
在Rt△DFG中,DG![]()
![]()
故二面角C―AB―D的平面角的余弦值为![]()


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
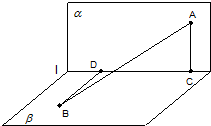 (2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,
(2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,查看答案和解析>>
科目:高中数学 来源: 题型:
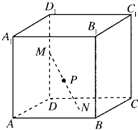 如图,已知正方体ABCD-A1B1C1D1的棱长为a(a>2),长度为2的线段MN的一个端点M在DD1上运动,另一端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为
如图,已知正方体ABCD-A1B1C1D1的棱长为a(a>2),长度为2的线段MN的一个端点M在DD1上运动,另一端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为查看答案和解析>>
科目:高中数学 来源:天利38套《2009高考模拟试题汇编附加试题》、数学理科 题型:044
如图长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,且AB与平面α,β所成的角都是30°,AC⊥l,垂足为C,BD⊥l,垂足为D.

(Ⅰ)求直线AB与CD所成角的大小;
(Ⅱ)求二面角C-AB-D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2006年广东省广州市高考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com