Question

【题目】在平面直角坐标系中，椭圆的离心率为,直线被椭圆截得的线段长为.

（1）求椭圆的方程；

（2）过原点的直线与椭圆交于两点（不是椭圆的顶点），点在椭圆上，且，直线与轴轴分别交于两点.

①设直线斜率分别为，证明存在常数使得，并求出的值；

②求面积的最大值.

Answer 1

【答案】(1).

(2) ①证明见解析，；②.

【解析】试题分析：（1）首先由题意得到，即.

将代入可得，

由，可得.得解.

（2）（ⅰ）注意从确定的表达式入手，探求使成立的.

设，则，

得到，

根据直线BD的方程为，

令，得，即.得到.

由，作出结论.

（ⅱ）直线BD的方程，

从确定的面积表达式入手，应用基本不等式得解.

试题解析：（1）由题意知，可得.

椭圆C的方程可化简为.

将代入可得，

因此，可得.

因此，

所以椭圆C的方程为.

（2）（ⅰ）设，则，

因为直线AB的斜率，

又，所以直线AD的斜率，

设直线AD的方程为，

由题意知，

由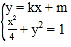，可得.

所以，

因此，

由题意知，

所以，

所以直线BD的方程为，

令，得，即.

可得.

所以，即.

因此存在常数使得结论成立.

（ⅱ）直线BD的方程，

令，得，即，

由（ⅰ）知，

可得的面积，

因为，当且仅当时等号成立，

此时S取得最大值，

所以的面积的最大值为.