
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
分析 (1)根据所给的表格求出本组数据的样本中心点,利用公式法求出b的值,结合样本中心点在线性回归直线上求得a值,从而得出回归直线方程;
(2)根据所给的x的值,代入线性回归方程,求出相应的y,再代入公式,即可得出结论.
解答 解:(1)由题意得$\overline{x}$=10,$\overline{y}$=40,b=$\frac{1190-4×10×40}{594-4×100}$≈-2,a=40-(-2)×10=60,
所以线性回归方程为y=-2x+60.
(2)由(1)得y1=24,y2=34,y3=40,y4=62,
∴R2=1-$\frac{0+0+4+4}{256+36+4+576}$=$\frac{108}{109}$≈0.99,
这表明平均气温解释了99%的用电量变化,且该模型的拟合效果好.
点评 本题考查回归直线方程,考查回归分析的初步应用.解答的关键是利用直接法求出回归直线方程.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 3$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
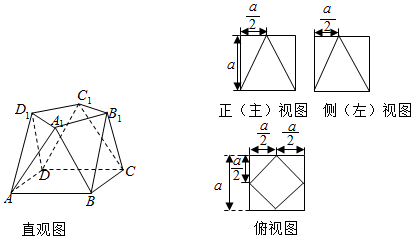
| A. | 3a2 | B. | 5a2 | C. | $\frac{9}{2}$a2 | D. | $\frac{11}{2}$a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,-1) | C. | (1,0) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 家庭编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,0,1) | (1,2,1) | (1,2,2) | (1,1,1) | (1,2,2) | (1,2,1) | (1,1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com