
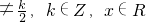 },且f(x)+f(2-x)=0,f(x+1)=-
},且f(x)+f(2-x)=0,f(x+1)=- ,当
,当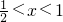 时:f(x)=3x.
时:f(x)=3x. )上的表达式;
)上的表达式; ,2k+1)时,log3f(x)>x2-kx-2k有解,并说明理由.
,2k+1)时,log3f(x)>x2-kx-2k有解,并说明理由.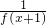 =f(x),
=f(x), )?-x∈(-
)?-x∈(- ,0)?1-x∈(
,0)?1-x∈( ,1).
,1).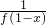
 .…
.… ,2k+1)?x-2k∈(
,2k+1)?x-2k∈( ,1),
,1), ,2k+1)上有解(k∈N+),
,2k+1)上有解(k∈N+), ,2k+1)≠∅,
,2k+1)≠∅, ,无解.
,无解. ,得到周期为2;再结合f(x)+f(2-x)=0即可判断f(x)的奇偶性;
,得到周期为2;再结合f(x)+f(2-x)=0即可判断f(x)的奇偶性; )?-x∈(-
)?-x∈(- ,0)?1-x∈(
,0)?1-x∈( ,1);再结合奇函数的性质以及当
,1);再结合奇函数的性质以及当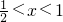 时:f(x)=3x即可得到结论;
时:f(x)=3x即可得到结论; ,2k+1)上有解(k∈N+),得到(0,k+1)∩(2k+
,2k+1)上有解(k∈N+),得到(0,k+1)∩(2k+ ,2k+1)≠∅,即可求出结论.
,2k+1)≠∅,即可求出结论.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
| x+y |
| 1+xy |
| 1-x |
| 1+x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x-y |
| 1-xy |
| 1 |
| 2 |
| 2an | ||
1+
|
| 1 |
| g(n) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com