
【题目】如图,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=1,CD=2,若将△BCD沿着BD折起至△BC'D,使得AD⊥BC'.

(1)求证:平面C'BD⊥平面ABD;
(2)求C'D与平面ABC'所成角的正弦值;
(3)M为BD中点,求二面角M﹣AC'﹣B的余弦值.
【答案】(1)见解析(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先证明![]() 、
、![]() ,再利用面面垂直的判定即可得证;
,再利用面面垂直的判定即可得证;
(2)先证明![]() 面
面![]() ,再求
,再求![]() 即可得解;
即可得解;
(3)建立空间坐标系,分别求出两面的法向量即可得解.
(1)过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,得
,得![]() ,
,![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴平面
,∴平面![]() ⊥平面
⊥平面![]() ;
;
(2)由(1)![]() 平面
平面![]() ,可知:平面
,可知:平面![]() ⊥平面
⊥平面![]() ,
,
又![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 面
面![]() ,∴
,∴![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
由(1)![]() 平面
平面![]() 可知:
可知:![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ;
;
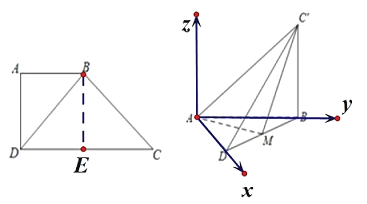
(3)以![]() 为原点,
为原点,![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,由(1)
轴建立如图所示的空间直角坐标系,由(1)![]() 可知,
可知,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴平面![]() 的一个法向量
的一个法向量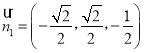 ,
,
平面![]() 的一个法向量
的一个法向量![]() ,
,
∴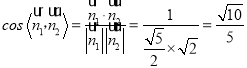 ,
,
由图可知二面角![]() 的大小为锐角,
的大小为锐角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次函数f(x)=ax2﹣2bx+8.
(1)设集合P={1,2,3}和Q={2,3,4,5},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间(﹣∞,2]上有零点且为减函数的概率?
(2)设集合P=[1,3]和Q[2,5],分别从集合P和Q中随机取一个实数作为a和b,求函数y=f(x)在区间(﹣∞,2]上有零点且为减函数的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
(1)求椭圆C的标准方程;
(2)求椭圆C上的点到直线l:4x﹣5y+40=0的最小距离?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解学生对消防知识的了解情况,从高一年级和高二年级各选取100名同学进行消防知识竞赛.下图(1)和图(2)分别是对高一年级和高二年级参加竞赛的学生成绩按![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
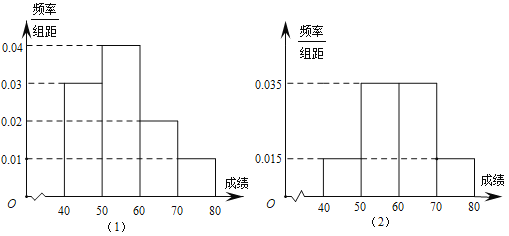
(1)请计算高一年级和高二年级成绩小于60分的人数;
(2)完成下面![]() 列联表,并回答:有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”?
列联表,并回答:有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
高一 | |||
高二 | |||
合计 |
附:临界值表及参考公式:![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,过焦点且垂直于x轴的直线被椭圆截得的线段长为3
,过焦点且垂直于x轴的直线被椭圆截得的线段长为3
(1)求椭圆的方程;
(2)已知P为直角坐标平面内一定点,动直线l:![]() 与椭圆交于A、B两点,当直线PA与直线PB的斜率均存在时,若直线PA与PB的斜率之和为与t无关的常数,求出所有满足条件的定点P的坐标.
与椭圆交于A、B两点,当直线PA与直线PB的斜率均存在时,若直线PA与PB的斜率之和为与t无关的常数,求出所有满足条件的定点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司近年来科研费用支出![]() 万元与公司所获得利润
万元与公司所获得利润![]() 万元之间有如下的统计数据:
万元之间有如下的统计数据:
x | 2 | 3 | 4 | 5 |
Y | 18 | 27 | 32 | 35 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
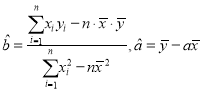
参考数据:2×18+3×27+4×32+5×35=420
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,长轴长为4,离心率为
,长轴长为4,离心率为![]() .过右焦点
.过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(均不与
两点(均不与![]() 重合),记直线
重合),记直线![]()
![]() 的斜率分别为
的斜率分别为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在常数![]() ,当直线
,当直线![]() 变动时,总有
变动时,总有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com