
����Ŀ��ijУΪ���˽�ѧ��������֪ʶ���˽�������Ӹ�һ�꼶�߶��꼶��ѡȡ100��ͬѧ��������֪ʶ����.��ͼ��1����ͼ��2���ֱ��ǶԸ�һ�꼶�߶��꼶�μӾ�����ѧ���ɼ���![]() ���飬�õ���Ƶ�ʷֲ�ֱ��ͼ.
���飬�õ���Ƶ�ʷֲ�ֱ��ͼ.
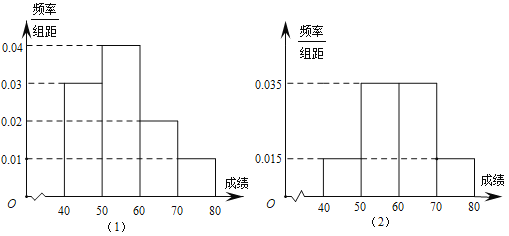
��1��������һ�꼶�߶��꼶�ɼ�С��60�ֵ�������
��2���������![]() �����������ش��ж��İ��տ�����Ϊ��ѧ�����ڵ��꼶��������ʶ���˽��������ԡ���
�����������ش��ж��İ��տ�����Ϊ��ѧ�����ڵ��꼶��������ʶ���˽��������ԡ���
�ɼ�С��60������ | �ɼ���С��60������ | �ϼ� | |
��һ | |||
�߶� | |||
�ϼ� |
�����ٽ�ֵ�����ο���ʽ��![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1����һ�꼶�ɼ�С��60�ֵ�����Ϊ70�ˣ���һ�꼶�ɼ�С��60�ֵ�����Ϊ50�ˣ���2����![]() �İ�����Ϊ��ѧ�����ڵ��꼶��������ʶ���˽��������ԡ�
�İ�����Ϊ��ѧ�����ڵ��꼶��������ʶ���˽��������ԡ�
��������
��1������Ƶ�ʷֲ�������ɵø�һ�꼶�߶��꼶�ɼ�С��60�ֵ�������
��2����д![]() ������������
������������![]() ��ֵ�����������ɵý���.
��ֵ�����������ɵý���.
�⣺��1����һ�꼶�ɼ�С��60�ֵ�����Ϊ��![]() ��
��
��һ�꼶�ɼ�С��60�ֵ�����Ϊ��![]() ��
��
��2��![]() ���������£�
���������£�
�ɼ�С��60������ | �ɼ���С��60������ | �ϼ� | |
��һ | 70 | 30 | 100 |
�߶� | 50 | 50 | 100 |
�ϼ� | 120 | 80 | 200 |
�ɵã�![]()
������![]() �İ�����Ϊ��ѧ�����ڵ��꼶��������ʶ���˽��������ԡ�.
�İ�����Ϊ��ѧ�����ڵ��꼶��������ʶ���˽��������ԡ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ����
����![]() ��ֵ��
��ֵ��
��2����֪ij���![]() �ˣ�����
�ˣ�����![]() ������������������ͬ�ĸ���Ϊ
������������������ͬ�ĸ���Ϊ![]() ��
��![]() ����һ�꿴��365��.
����һ�꿴��365��.
��i����![]() �ı���ʽ��
�ı���ʽ��
��ii������![]() �Ľ���ֵ����ȷ��0.01��.
�Ľ���ֵ����ȷ��0.01��.
�ο���ֵ��![]() ��
��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0����a��1������P������f��x����logax�ڣ�0��+������Ϊ������������Q������g��x����x2��2ax+4����㣮
��1��������P��Q����P��Q�٣���ʵ��a��ȡֵ��Χ��
��2������S������y��f��g��x����������[2��+������ֵ��Ϊ������������SΪ�����⣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��![]() 1���ҽ���ΪF1��F2ֱ�ߣ�
1���ҽ���ΪF1��F2ֱ�ߣ�![]() 1��x
1��x![]() y
y![]() 0�����Բ��һ����������y���ϣ���һ�������������Ϊ��m��1����
0�����Բ��һ����������y���ϣ���һ�������������Ϊ��m��1����
��1������ԲC�ķ��̣�
��2����PΪ��ԲC����һ�㣬������F1��F2���ҷֱ�ΪPM��PN����![]() ��1
��1![]() ��2
��2![]() ������1+��2��ֵ��
������1+��2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
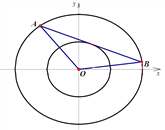
����Ŀ���ǽ�����ͬһ����������������ͬ����ԲΪ��������Բ��.��֪��Բ![]() ������Բ
������Բ![]() �Ľ���Ϊ������������Բ
�Ľ���Ϊ������������Բ![]() .
.
(��)����Բ![]() �ķ��̣�
�ķ��̣�
(��)��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ���㣬������Բ
���㣬������Բ![]() ����һ�������㣬���ж�
����һ�������㣬���ж�![]() ������Ƿ�Ϊ��ֵ(
������Ƿ�Ϊ��ֵ(![]() Ϊ����ԭ��)�����ǣ�����ö�ֵ�������ǣ���˵������.
Ϊ����ԭ��)�����ǣ�����ö�ֵ�������ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ţ�2040818101747712
����ţ�2050752239689728
�����ģ�
��ƽ��ֱ������ϵ�У�������ԭ��OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ.��ֱ֪��![]() �IJ�������Ϊ
�IJ�������Ϊ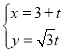 ��
��![]() Ϊ������������C�ļ����귽��Ϊ
Ϊ������������C�ļ����귽��Ϊ![]() .
.
��1��������![]() ��ֱ�����귽�̺�ֱ��
��ֱ�����귽�̺�ֱ��![]() ����ͨ���̣�
����ͨ���̣�
��2����ֱ��![]() ������
������![]() ����
����![]() ���㣬��
���㣬��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABCD�У�AB��CD����BAD��90����AB��AD��1��CD��2��������BCD����BD��������BC'D��ʹ��AD��BC'��

��1����֤��ƽ��C'BD��ƽ��ABD��
��2����C'D��ƽ��ABC'���ɽǵ�����ֵ��
��3��MΪBD�е㣬������M��AC'��B������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() =2cos����x
=2cos����x![]() ������>0�����㣺f��
������>0�����㣺f��![]() ��=f��
��=f��![]() �����������䣨
�����������䣨![]() ��
��![]() ���������ֵ��û����Сֵ�����������ĸ����⣺P1��
���������ֵ��û����Сֵ�����������ĸ����⣺P1��![]() ��[0��2��]�ϵ����ݼ���P2��
��[0��2��]�ϵ����ݼ���P2��![]() ����С��������4����P3��
����С��������4����P3��![]() ��ͼ�����ֱ��x
��ͼ�����ֱ��x![]() �Գƣ�P4��
�Գƣ�P4��![]() ��ͼ����ڵ㣨
��ͼ����ڵ㣨![]() ��0���Գ�.���е���������( )
��0���Գ�.���е���������( )
A.P1��P2B.P2��P4C.P1��P3D.P3��P4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() �ֱ�Ϊ˫����
�ֱ�Ϊ˫����![]()
![]()
![]() �����ҽ��㣬��P����
�����ҽ��㣬��P����![]() Ϊֱ����Բ��C�ڵ�һ�����ڵĽ��㣬���߶�
Ϊֱ����Բ��C�ڵ�һ�����ڵĽ��㣬���߶�![]() ���е�Q��C�Ľ������ϣ���C�����������߷���Ϊ__________��
���е�Q��C�Ľ������ϣ���C�����������߷���Ϊ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com