
“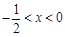 ”是“不等式
”是“不等式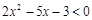 成立”的 条件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中选一个填写).
成立”的 条件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中选一个填写).
 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:填空题
设命题p:非零向量a,b,|a|=|b|是(a+b)⊥(a-b)的充要条件;命题q:平面上M为一动点,A,B,C三点共线的充要条件是存在角α,使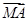 =sin2α
=sin2α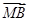 +cos2α
+cos2α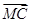 ,下列命题①p∧q;②p∨q;③¬p∧q;④¬p∨q.
,下列命题①p∧q;②p∨q;③¬p∧q;④¬p∨q.
其中假命题的序号是________.(将所有假命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列四个命题:
①命题“?x∈R,cos x>0”的否定是:“?x∈R,cos x≤0”;
②若lga+lgb=lg(a+b),则a+b的最大值为4;
③定义在R上的奇函数f(x)满足f(x+2)=-f(x),则f(6)的值为0;
④已知随机变量X服从正态分布N(1,σ2),P(X≤5)=0.81,则P(X≤-3)=0.19;其中真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列说法:
(1)命题“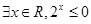 ”的否定是“
”的否定是“ ”;
”;
(2)关于 的不等式
的不等式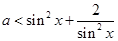 恒成立,则
恒成立,则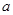 的取值范围是
的取值范围是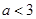 ;
;
(3)对于函数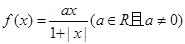 ,则有当
,则有当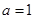 时,
时,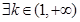 ,使得函数
,使得函数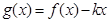 在
在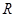 上有三个零点;
上有三个零点;
(4)已知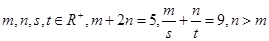 ,且
,且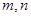 是常数,又
是常数,又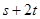 的最小值是
的最小值是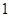 ,则
,则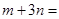 7.
7.
其中正确的个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com