
���� ��1��������ɵ�f��x��=R��x��-G��x������x����0��x��5��x��5���ɵõ���
��2���ֱ�����0��x��5��x��5�ĺ����ĵ����ԣ����ɵõ����ֵ��
��� �⣺��1���������G��x��=3+x��
��R��x��=$\left\{\begin{array}{l}{-0.4{x}^{2}+4.2x+0.2��0��x��5��}\\{11.2��x��5��}\end{array}\right.$��
��f��x��=R��x��-G��x��=$\left\{\begin{array}{l}{-0.4{x}^{2}+3.2x-2.8��0��x��5}\\{8.2-x��x��5}\end{array}\right.$��
��2����x��5ʱ���ߺ���y=f��x���ݼ���
��f��x����8.2-5=3.2����Ԫ����
��0��x��5ʱ��f��x��=-0.4��x-4��2+3.6��
��x=4ʱ��f��x�������ֵΪ3.6����Ԫ����
�𣺵���������4��̨ʱ����ʹӮ�����Ϊ3.6����Ԫ����
���� ���⿼��ֶκ����������ã����Ժ���ֵ������һ�κ����Ͷ��κ����ĵ����Լ���ֵ�����ڻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������p��x��R��x2-x-1��0����Vp��x��R��x2-x-1��0�� | |
| B�� | ���⣺����x2=1����x=1��x=-1������������ǣ�����x��1��x��-1����x2��1�� | |
| C�� | ��$��=\frac{��}{2}$���ǡ�y=sin��2x+�գ�Ϊż�������ij�Ҫ���� | |
| D�� | ����p����$\overrightarrow{a}$=��2��1����$\overrightarrow{b}$=��-1��k2-2������k=2��$\overrightarrow{a}��\overrightarrow{b}$�ij�ֲ���Ҫ����������q�����ݺ���f��x��=xa��a��R����ͼ����㣨2��$\frac{\sqrt{2}}{2}$������f��4��=$\frac{1}{2}$����p�ţ��Vq���Ǽ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
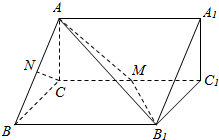 ��ͼ����ֱ������ABC-A1B1C1�У�AC��BC��CC1=4��M����CC1���е㣮
��ͼ����ֱ������ABC-A1B1C1�У�AC��BC��CC1=4��M����CC1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
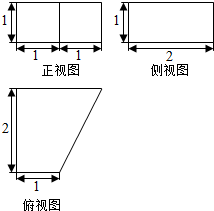 һ�������������ͼ��ͼ��ʾ��
һ�������������ͼ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com