
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由f (2+t)=f (2-t) 知函数函数图象关于x=2对称,再分别判断,即可得出结论.
解答 解:对于(1),∵函数f (x)=ax2+bx+c对任意实数t都有f (2+t)=f (2-t)成立
∴函数图象关于x=2对称,∴-$\frac{b}{2a}$=2,∴b=-4a,即(1)正确;
对于(2),∵当a>0且$\frac{m+n}{2}$>2时,m-2>2-n,∴f(x)在区间[n,m]上的最大值为f(m),即(2)正确;
对于(3),当a>0时f($\frac{5}{2}$)最小,当a<0时f(-1)最小,所以f(1)不可能最小的,即(3)正确.
故选:D.
点评 本题考查二次函数的性质和应用,解题时要注意函数f(x)=ax2+bx+c(a≠0)的对称轴是x=2.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
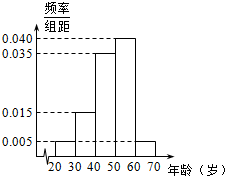 跳广场舞是现在广大市民喜爱的户外健身运动,某健身运动公司为了解本地区市民对跳广场舞的热衷程度,随机抽取了100名跳广场舞的市民,统计其年龄(单位:岁)并整理得到如下的频率分布直方图(其中年龄的分组区间分别为[20,30),[30,40),[40,50),[50,60),[60,70]),其中女性市民有55名,将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”.已知其中有30名女性广舞迷.
跳广场舞是现在广大市民喜爱的户外健身运动,某健身运动公司为了解本地区市民对跳广场舞的热衷程度,随机抽取了100名跳广场舞的市民,统计其年龄(单位:岁)并整理得到如下的频率分布直方图(其中年龄的分组区间分别为[20,30),[30,40),[40,50),[50,60),[60,70]),其中女性市民有55名,将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”.已知其中有30名女性广舞迷.| 广舞迷 | 非广舞迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2kπ-$\frac{π}{4}$,2kπ+$\frac{π}{4}$](k∈Z) | B. | [kπ,kπ+$\frac{π}{4}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | D. | [kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
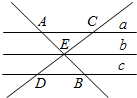 如图所示,a∥b∥c,直线AB与a、b、c分别相交于A、E、B,直线CD与a、b、c分别相交于C、E、D,AE=EB,则有( )
如图所示,a∥b∥c,直线AB与a、b、c分别相交于A、E、B,直线CD与a、b、c分别相交于C、E、D,AE=EB,则有( )| A. | AE=CE | B. | BE=DE | C. | CE=DE | D. | CE>DE |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
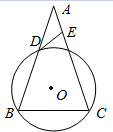 如图,圆O的半径为2,等腰△ABC的底边的两端点B,C在圆O上,AB与圆O交于点D,AD=2,圆O的切线DE交AC于E点.
如图,圆O的半径为2,等腰△ABC的底边的两端点B,C在圆O上,AB与圆O交于点D,AD=2,圆O的切线DE交AC于E点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com