
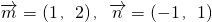
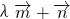 与
与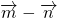 平行,求实数λ的值;
平行,求实数λ的值;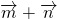 在
在 上的投影.
上的投影.科目:高中数学 来源: 题型:
| b |
| a |
| a′ |
| a |
2(
| ||||
|
|
| b |
| a |
| b |
| a′ |
| b |
| a |
| a′ |
| b |
| a |
| a′ |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AC |
| AB |
| AD |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| AC |
| AB |
| AD |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:上海 题型:解答题
| b |
| a |
| a′ |
| a |
2(
| ||||
|
|
| b |
| a |
| b |
| a′ |
| b |
| a |
| a′ |
| b |
| a |
| a′ |
| b |
查看答案和解析>>
科目:高中数学 来源:2010年上海市春季高考数学试卷(解析版) 题型:解答题
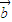 ,对任意向量
,对任意向量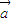 ,定义
,定义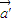 =
=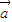 -
-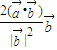 .
.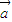 =(2,3),
=(2,3),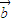 =(-1,3),求
=(-1,3),求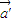 ;
;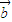 =(2,1),证明:若位置向量
=(2,1),证明:若位置向量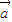 的终点在直线Ax+By+C=0上,则位置向量
的终点在直线Ax+By+C=0上,则位置向量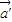 的终点也在一条直线上;
的终点也在一条直线上;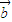 ,当位置向量
,当位置向量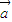 的终点在抛物线C:x2=y上时,位置向量
的终点在抛物线C:x2=y上时,位置向量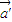 终点总在抛物线C′:y2=x上,曲线C和C′关于直线l对称,问直线l与向量
终点总在抛物线C′:y2=x上,曲线C和C′关于直线l对称,问直线l与向量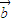 满足什么关系?
满足什么关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com