练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知平面上三个向量a、b、c的模均为1，它们相互之间的夹角均为．

    (Ⅰ)求证：(a－b)⊥c；

    (Ⅱ)若|ka＋b＋c|＞1(k∈R)，求k的取值范围．

    答案：
    解析：

    		 　　解：(Ⅰ)∵|a|＝|b|＝|c|＝1，且a、b、c之间的夹角均为 ，

    　　解：(Ⅰ)∵|a|＝|b|＝|c|＝1，且a、b、c之间的夹角均为，

    　　∴(a－b)·c＝a·c－b·c＝|a||c|－|b||c|＝0，

    　　∴(a－b)⊥c．

    　　(Ⅱ)∵|ka＋b＋c|＞1，∴|ka＋b＋c|2＞1，

    　　∴(ka＋b＋c)·(ka＋b＋c)＞1，

    　　∴k2a·a＋b·b＋c·c＋2ka·b＋2ka·c＋2b·c＞1，

    　　∵a·b＝a·c＝b·c＝＝－，∴k2－2k＞0．

    　　∴k＜0或k＞2．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知△ABC在平面α内，DA⊥α，DC与α成角，且DC⊥BC，若EB＝BC＝DC＝a，求DE的长．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知平面上三个向量a、b、c的模均为1，它们相互之间的夹角均为．

    (Ⅰ)求证：(a－b)⊥c；

    (Ⅱ)若|ka＋b＋c|＞1(k∈R)，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知M、N是两个平行平面，在M内取4个点，在N内取5个点，这9个点中再无其他4点共面，则

    (1)这些点最多能确定几个平面？

    (2)以这些点为顶点，能作多少个四棱锥，多少个三棱锥？

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：047

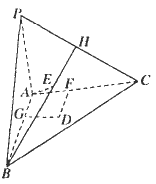
    已知：平面PAB⊥平面ABC，平面PAC⊥平面ABC，F是点A在平面PBC内的射影．

    (1)求证：PA⊥平面ABC；

    (2)当E为△PBC的垂心时，求证：△ABC是直角三角形．

    查看答案和解析>>

    同步练习册答案