
���� �٣���m=1ʱ������x2+my2=1��ʾԲ��
�ڣ���a=��1ʱ��ֱ��l1��ֱ��l2��ƽ�У�
�ۣ�������f ��x��=x3+mx��������⇒m��0��
�ܣ�p��q��������⇒p��q��һ���������⣻⇒p��q��������⇒p��qһ���������⣻
��� �⣺���ڢ٣���m=1ʱ������x2+my2=1��ʾԲ���ʴ���
���ڢڣ���a=��1ʱ��ֱ��l1��ֱ��l2��ƽ�У�����ȷ��
���ڢۣ�������f ��x��=x3+mx��������⇒m��0���ʴ���
���ڢܣ�p��q��������⇒p��q��һ���������⣻⇒p��q��������⇒p��qһ���������⣬����ȷ��
�ʴ�Ϊ���ڢ�
���� ���⿼�����������٣����ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=|lnx| | B�� | y=-lnx | C�� | y=2-x | D�� | y=2|x| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{3}$ | B�� | $\frac{3}{5}$ | C�� | ∁UA��∁UB | D�� | $-\frac{3}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | $-\frac{��}{4}$ | $\frac{��}{12}$ | $\frac{5��}{12}$ | $\frac{3��}{4}$ | $\frac{13��}{12}$ |
| ��x+ϕ | 0 | $\frac{��}{2}$ | �� | $\frac{3��}{2}$ | 2�� |
| f��x�� | 2 | 6 | 2 | -2 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
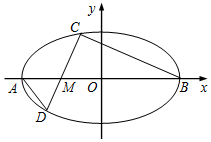 ��ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����������ֱ�ΪA��-a��0����B��a��0������M��-1��0������3$\overrightarrow{AM}$=$\overrightarrow{MB}$������Mб��Ϊk��k��0����ֱ�߽���ԲE��C��D���㣬���е�C��x���Ϸ���
��ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����������ֱ�ΪA��-a��0����B��a��0������M��-1��0������3$\overrightarrow{AM}$=$\overrightarrow{MB}$������Mб��Ϊk��k��0����ֱ�߽���ԲE��C��D���㣬���е�C��x���Ϸ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\sqrt{5}$ | C�� | $\frac{5}{2}$ | D�� | $\frac{\sqrt{10}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
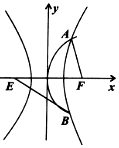 ��֪E��FΪ˫����$C��\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$�����ҽ��㣬������y2=2px��p��0����˫�����й����Ľ���F������˫���߽��ڲ�ͬ������A��B����$|AF|=\frac{4}{5}|BE|$����˫���ߵ�������Ϊ$4��\sqrt{7}$��
��֪E��FΪ˫����$C��\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$�����ҽ��㣬������y2=2px��p��0����˫�����й����Ľ���F������˫���߽��ڲ�ͬ������A��B����$|AF|=\frac{4}{5}|BE|$����˫���ߵ�������Ϊ$4��\sqrt{7}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com