
| A. | $(1,2+\frac{2}{e})$ | B. | $(2,2+\frac{2}{e})$ | C. | $(1,1+\frac{1}{e})$ | D. | $(2,2+\frac{1}{e})$ |
分析 求出f(x)=e-a+$\frac{a}{2}$的解为1-a,即可得出f(x)=a-1有三解,判断f(x)的单调性,计算最值,作出f(x)的图象,根据图象得出关于a的不等式,即可解出a的范围.
解答 解:当x<0时,f(x)在(-∞,0)上单调递增,且x→-∞时,f(x)→$\frac{a}{2}$,
当x≥0时,f′(x)=ex-1+ax-a-1,
∴f′(x)是增函数,且f′(1)=0,
∴当0<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
又f(1)=0,当x→+∞时,f(x)→+∞,
作出f(x)的大致函数图象如图所示: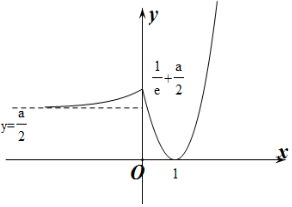
由图象可知f(x)≥0,∴f(-f(x))∈($\frac{a}{2}$,$\frac{1}{e}+\frac{a}{2}$],
∴$\frac{a}{2}$<e-a+$\frac{a}{2}$≤$\frac{1}{e}$+$\frac{a}{2}$,
解得a≥1.
令-f(x)=t,则t≤0,且f(t)=e-a+$\frac{a}{2}$,
由图象可知:f(t)=e-a+$\frac{a}{2}$有三解,不妨设从小到大依次为t1,t2,t3,
则t1=1-a,t3>1>t2>0不符合题意,舍去.
∴-f(x)=1-a,即f(x)=a-1.
∴f(x)=a-1有三解,
∴$\frac{a}{2}<a-1<\frac{1}{e}+\frac{a}{2}$,解得2$<a<2+\frac{2}{e}$.
故选B.
点评 本题考查了函数零点与函数图象的关系,函数单调性的判断与极值计算,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1365石 | B. | 338 石 | C. | 168石 | D. | 134石 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com