
若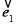 ,
,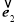 ,
,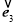 为同一平面内互不共线的三个单位向量,并满足
为同一平面内互不共线的三个单位向量,并满足 +
+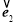 +
+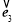 =
=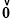 ,且向量
,且向量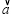 =x
=x +
+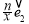 +(x+
+(x+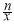 )
)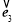 (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求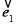 与
与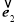 所成角的大小;
所成角的大小;
(2)记f(x)=|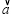 |,试求f(x)的单调区间及最小值.
|,试求f(x)的单调区间及最小值.
(1)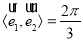 ;
;
(2)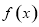 的减区间为
的减区间为 和
和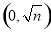 ;再由均值不等式易求得:
;再由均值不等式易求得: 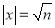 时,
时,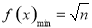 .
.
【解析】
试题分析:(1)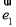 与
与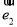 所成角的大小,首先求出向量
所成角的大小,首先求出向量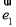 与
与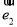 的数量积,由已知
的数量积,由已知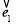 +
+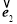 +
+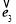 =
=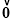 ,可得
,可得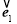 +
+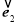 =-
=-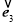 ,两边平方可得
,两边平方可得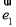 与
与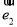 的数量积,再利用函数的数量积求出向量的夹角.(2)求
的数量积,再利用函数的数量积求出向量的夹角.(2)求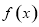 的单调区间及最小值,首先把向量的模长转化为求向量的数量积,得函数
的单调区间及最小值,首先把向量的模长转化为求向量的数量积,得函数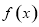 的解析式,进一步利用导数求出单调区间,最后确定最值.
的解析式,进一步利用导数求出单调区间,最后确定最值.
试题解析:(1)依题设:|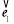 |=|
|=|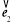 |=|
|=|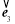 |=1,且
|=1,且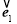 +
+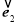 =-
=-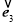 ⇒ (
⇒ (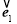 +
+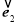 )2=(-
)2=(-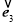 )2,化简得:
)2,化简得:
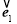 ·
·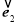 =-
=-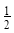 ⇒ cos<
⇒ cos<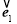 ,
,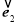 >=-
>=-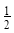 ,又<
,又<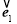 ,
,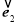 >∈[0, π] ⇒ <
>∈[0, π] ⇒ <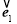 ,
,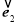 >=
>=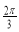 .
.
(2)由 (1)易知: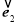 ·
·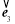 =
=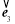 ·
·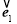 =
=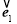 ·
·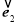 =-
=-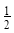 ,故由f(x)=|
,故由f(x)=| |=
|=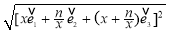 ,将其展开整理得: f(x)=
,将其展开整理得: f(x)=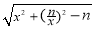 (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
①x>0时,对u(x)=x2+(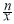 )2-n,求导并整理得:
)2-n,求导并整理得: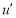 (x)=
(x)= .则由
.则由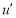 (x)>0⇒x>
(x)>0⇒x> ,且由
,且由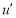 (x)<0⇒0<x<
(x)<0⇒0<x< .即f(x)的增区间为(
.即f(x)的增区间为( , +∞),减区间为(0,
, +∞),减区间为(0,  ).
).
②x<0时,因f(x)为偶函数,由图像的对称性知:f(x)的增区间为(- ,0),减区间为(-∞,-
,0),减区间为(-∞,- ).
).
综上:f(x)的增区间为 (- ,0) 与 (
,0) 与 ( , +∞),f(x)的减区间为(-∞, -
, +∞),f(x)的减区间为(-∞, - ) 和 (0,
) 和 (0,  ).
).
再由均值不等式易求得:|x|= 时, f(x)min=
时, f(x)min= .
.
考点:向量的数量积,向量的夹角,向量的模,均值不等式,利用导数求函数的单调区间和最值.


科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
若各项均为正数的等比数列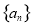 满足
满足 其前
其前 项的和为
项的和为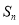 ,则
,则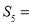 ( )
( )
A.31 B.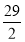 C.
C.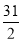 D.以上都不对
D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三10月月考理科数学试卷(解析版) 题型:选择题
使函数f(x)=sin(2x+θ)+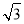 cos(2x+θ)是奇函数,且在区间
cos(2x+θ)是奇函数,且在区间 上是减函数的θ的一个值是 ( )
上是减函数的θ的一个值是 ( )
A.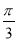 B.
B.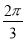 C.
C.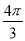 D.
D.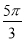
查看答案和解析>>
科目:高中数学 来源:2015届江西省红色六校高三第一次联考文科数学试卷(解析版) 题型:选择题
在平面直角坐标系中,两点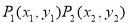 间的“L-距离”定义为
间的“L-距离”定义为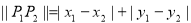 ,则平面内与
,则平面内与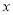 轴上两个不同的定点
轴上两个不同的定点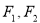 的“L-距离”之和等于定值(大于
的“L-距离”之和等于定值(大于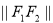 )的点的轨迹可以是( )
)的点的轨迹可以是( )
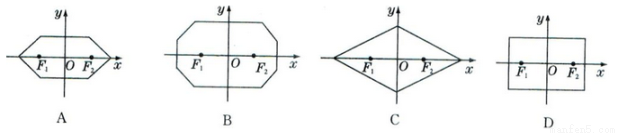
查看答案和解析>>
科目:高中数学 来源:2015届江西省红色六校高三第一次联考文科数学试卷(解析版) 题型:选择题
随机掷两枚质地均匀的骰子,它们向上的点数之和不超过4的概率记为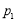 ,点数之和大于8的概率记为
,点数之和大于8的概率记为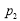 ,点数之和为奇数的概率记为
,点数之和为奇数的概率记为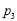 ,则 ( )
,则 ( )
A.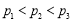 B.
B.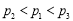
C.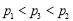 D.
D.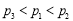
查看答案和解析>>
科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:填空题
若等腰△ABC底边BC上的中线长为1,底角B>60º,则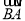 ·
·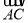 的取值范围是______.
的取值范围是______.
查看答案和解析>>
科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:选择题
已知 ,
, 是不共线的向量,若
是不共线的向量,若 =λ
=λ +
+ ,
, =
= +μ
+μ (λ,μ∈R),则A, B, C三点共线的充要条件是:( )
(λ,μ∈R),则A, B, C三点共线的充要条件是:( )
A.λ+μ=1 B.λ-μ=1 C.λμ=1 D.λμ=-1
查看答案和解析>>
科目:高中数学 来源:2015届江苏省连云港高二下学期期末数学试卷(选修物理)(解析版) 题型:填空题
将1、2、3、4、5、6、7、8、9这9个正整数分别写在三张卡片上,要求每一张卡片上的三个数字中任意两数之差都不在这张卡片上.现在第一张卡片上已经写有1和5,第二张卡片上写有2,第三张卡片上写有3,则第一张卡片上的另外一个数字是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com