
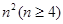 个正数排成
个正数排成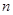 行
行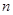 列:
列:
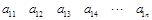
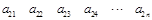
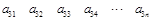
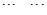
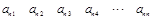
其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知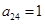 ,
,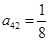 ,
,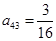 ,则
,则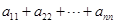 = 。
= 。
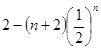
【解析】
试题分析:设a11=a,第一行数的公差为d,第一列数的公比为q,可得ast=[a+(t-1)d]qs-1,又设第一行数列公差为d,各列数列的公比为q,则第四行数列公差是dq3,于是可得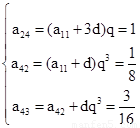 ,
,
解此方程组,得a11=d=q=±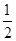 ,由于给n2个数都是正数,必有q>0,从而有a11=d=q=
,由于给n2个数都是正数,必有q>0,从而有a11=d=q=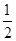 ,
,
于是对任意的1≤k≤n,有akk=a1kqk-1=[a11+(k-1)d]qk-1=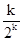 ,
,
得S=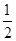 +
+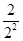 +……+
+……+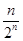 ,
,
又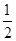 S=
S=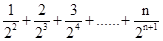 。
。
两式相减后得: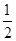 S=
S=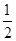 +
+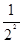 +……+
+……+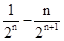 ,
,
所以S=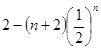 。
。
考点:本题主要考查等差数列、等比数列的基础知识,“错位相减法”。
点评:难题,通过观察数列的特征,布列方程组,先求出数列的通项,从而根据数列通项的特点选择合适的求和方法。“分组求和法”“裂项相消法”也常常考到的求和方法。


科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年北京东城区高三上学期文科数学综合练习(一) 题型:填空题
如图,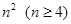 个正数排成
个正数排成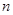 行
行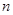 列方阵:符号
列方阵:符号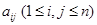 表示位于第
表示位于第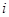 行第
行第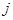 列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列的数的公比都等于
列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列的数的公比都等于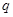 . 若
. 若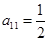 ,
,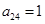 ,
,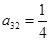 ,
则
,
则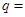 ________,
________,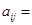 __________.
__________.

查看答案和解析>>
科目:高中数学 来源:2013届湖北省咸宁赤壁市期中新四校联考高一(理科)数学试卷 题型:解答题
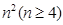 个正数排成
个正数排成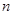 行
行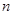 列:
列:
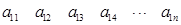
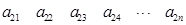
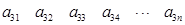
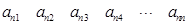
其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知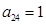 ,
,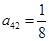 ,
,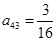 ,试求
,试求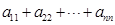 的值. (本题满分13分)
的值. (本题满分13分)
查看答案和解析>>
科目:高中数学 来源:2013届湖北省咸宁赤壁市期中新四校联考高一(文科)数学试卷 题型:解答题
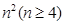 个正数排成
个正数排成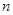 行
行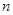 列:
列:
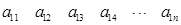
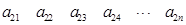
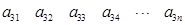
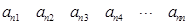
其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知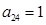 ,
,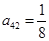 ,
,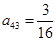 ,试求
,试求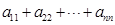 的值. (本题满分13分)
的值. (本题满分13分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com