练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某化工厂生产甲、乙两种肥料，生产1车皮甲种肥料能获得利润10000元，需要的主要原料是磷酸盐4吨，硝酸盐18吨；生产1车皮乙种肥料能获得利润5000元，需要的主要原料是磷酸盐1吨，硝酸盐15吨．现库存有磷酸盐10吨，硝酸盐66吨，在此基础上生产这两种肥料．问分别生产甲、乙两种肥料各多少车皮，能够获得最大利润？


    解：设生产甲种肥料x车皮、乙种肥料y车皮能够获得利润z万元．

    目标函数为z＝x＋0.5y，

    约束条件：，

    可行域如图中阴影部分内的整点．

    解方程组得：M点坐标为(2,2)．

    当直线y＝－2x＋2z经过可行域上的点M时，截距2z最大，即z最大．

    所以zmax＝x＋0.5y＝3.

    所以生产甲种、乙种肥料各2车皮，能够获得最大利润，最大利润为3万元．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    据科学计算，运载“神九”的“长征”二号F系列火箭在点火后第一秒钟通过的路程为2 km，以后每秒钟通过的路程增加2 km，在到达离地面240 km的高度时，火箭与飞船分离，则这一过程需要的时间为(　　)

    A．10秒钟                          B．13秒钟

    C．15秒钟                          D．20秒钟

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若a<0，则关于x的不等式x2－4ax－5a2>0的解是(　　)

    A．x>5a或x<－a　　　　　         B．x>－a或x<5a

    C．5a<x<－a                       D．－a<x<5a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知变量x，y满足约束条件，则z＝3x＋y的最大值为(　　)

    A．12                                B．11

    C．3                                 D．－1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    画出不等式组表示的平面区域，并回答下列问题：

    (1)指出x，y的取值范围；

    (2)平面区域内有多少个整点？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一切奇数都不能被2整数，2100＋1是奇数，所以2100＋1不能被2整除，其演绎“三段论”的形式为：

    大前提：一切奇数都不能被2整除，

    小前提：________________________________________________________________________，

    结论：________________________________________________________________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在圆中有结论：如图所示，“AB是圆O的直径，直线AC，BD是圆O过A，B的切线，P是圆O上任意一点，CD是过P的切线，则有PO2＝PC·PD”．类比到椭圆：“AB是椭圆的长轴，直线AC，BD是椭圆过A，B的切线，P是椭圆上任意一点，CD是过P的切线，则有____________．”

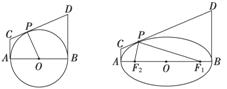
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知二次函数f(x)＝ax2＋bx＋c(a>0)的图象与x轴有两个不同的交点．若f(c)＝0，且0<x<c时，f(x)>0.

    (1)证明：是函数f(x)的一个零点；

    (2)试比较与c的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为(　　)

    A.π　　　　　　　　　　      B．4π

    C．4π                        D．6π

    查看答案和解析>>

    同步练习册答案