
下面是一段演绎推理:
如果直线平行于平面,则这条直线平行于平面内的所有直线;
已知直线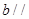 平面
平面 ,直线
,直线 平面
平面 ;
;
所以直线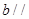 直线
直线 ,在这个推理中( )
,在这个推理中( )
| A.大前提正确,结论错误 |
| B.小前提与结论都是错误的 |
| C.大、小前提正确,只有结论错误 |
| D.大前提错误,结论错误 |
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:单选题
用反证法证明命题:若整数系数的一元二次方程 有有理实数根,那么
有有理实数根,那么 ,
, ,
, 中至少有一个是偶数,下列假设中正确的是( )
中至少有一个是偶数,下列假设中正确的是( )
A.假设 , , , , 都是偶数 都是偶数 |
B.假设 , , , , 都不是偶数 都不是偶数 |
C.假设 , , , , 至多有一个是偶数 至多有一个是偶数 |
D.假设 , , , , 至多有两个偶数 至多有两个偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
① ,这与三角形内角和为
,这与三角形内角和为 相矛盾,
相矛盾, 不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角
不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角 、
、 、
、 中有两个直角,不妨设
中有两个直角,不妨设 ,正确顺序的序号为
,正确顺序的序号为
| A.①②③ | B.③①② | C.①③② | D.②③① |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
圆周上2个点可连成1条弦,这条弦可将圆面划分成2部分;圆周上3个点可连成3条弦,这3条弦可将圆面划分成4部分;圆周上4个点可连成6条弦,这6条弦最多可将圆面划分成8部分.则这些弦最多可把圆面分成 ( ) 部分
| A.2n-1 | B.2n | C.2n+1 | D.2n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用数学归纳法证明“n3+(n+1)3+(n+2)3,(n∈N+)能被9整除”,要利
用归纳法假设证n=k+1时的情况,只需展开( ).
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,模块①~⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①~⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体,则下列选择方案中,能够完成任务的为( )
| A.模块①,②,⑤ | B.模块①,③,⑤ |
| C.模块②,④,⑤ | D.模块③,④,⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com