练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，底面，底面是直角梯形，为侧棱上一点，已知.

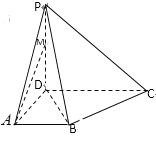
    （Ⅰ）证明:平面平面；

    （Ⅱ）求二面角的余弦值.

    【答案】（Ⅰ）证明见解析；（Ⅱ）.

    【解析】

    (Ⅰ) 先证明，再证明平面，利用面面垂直的判定定理，即可求证所求证；

    (Ⅱ)根据题意以为轴、轴、轴建立空间直角坐标系，求出平面和平面的向量，利用公式即可求解.

    (Ⅰ)证：由已知得

    又 平面，平面，，

    而故，平面

    平面，平面平面

    (Ⅱ)由(Ⅰ)知，推理知梯形中，，，

    有，又，故

    所以相似，故有，即

    所以，以为轴、轴、轴建立如图所示的空间直角坐标系，

    则

    ，，，设平面的法向量为，则

    令，则，是平面的一个法向量

    设平面的一个法向量为

    令，则

    是平面的一个法向量

    =

    又二面角为钝二面角，其余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在发生公共卫生事件期间，有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”.过去10日，A、B、C、D四地新增疑似病例数据信息如下：

    A地：中位数为2，极差为5； B地：总体平均数为2，众数为2；

    C地：总体平均数为1，总体方差大于0； D地：总体平均数为2，总体方差为3.

    则以上四地中，一定符合没有发生大规模群体感染标志的是_______(填A、B、C、D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市为了调查小区成年居民对环境治理情况的满意度（满分按100计），随机对20名六十岁以上的老人和20名十八岁以上六十岁以下的中青年进行了不记名的问卷调查，得到了如下统计结果：

    表1：六十岁以上的老人对环境治理情况的满意度与频数分布表

    满意度

    人数

    1

    5

    6

    5

    3

    表2：十八岁以上六十岁以下的中青年人对环境治理情况的满意度与频数分布表

    满意度

    人数

    2

    4

    8

    4

    2

    表3：

    满意度小于80

    满意度不小于80

    合计

    六十岁以上老人人数

    十八岁以上六十岁以下的中青年人人数

    合计

    （1）若该小区共有中青年人500人，试估计其中满意度不少于80的人数；

    （2）完成表3的列联表，并回答能否有的把握认为“小区成年居民对环境治理情况的满意度与年龄有关”？

    （3）从表3的六十岁以上的老人“满意度小于80”和“满意度不小于80”的人数中用分层抽样的方法抽取一个容量为5的样本，再从中任取3人，求至少有两人满意小于80的概率.

    附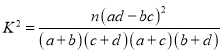：，其中.

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    0.455

    0.708

    1.323

    2.072

    2.706

    3.84

    5.024

    6.635

    7.879

    10.83

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知椭圆C：(a＞b＞0)的离心率为．且经过点(1，)，A，B分别为椭圆C的左、右顶点，过左焦点F的直线l交椭圆C于D，E两点（其中D在x轴上方）．

    （1）求椭圆C的标准方程；

    （2）若△AEF与△BDF的面积之比为1：7，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y（单位：万元／辆）进行整理，得到如下数据：

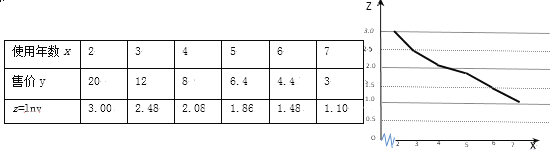
    如图是z关于x的折线图：

    （1）由折线图可以看出，可以用线性回归模型拟合z和x的关系，请用相关系数r加以说明（注：若相关系数︱r︱0.75，则认为两个变量相关程度较强）；

    （2）求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少？（小数点后面保留两位有效数字）；

    （3）基于成本的考虑，该型号二手车的售价不得低于7118元，请根据（2）求出的回归方程预测在收购该型号的二手车时车辆的使用年限不得超过多少年？

    参考公式：回归方程中斜率和截距的最小二乘法估计公式分别为：

    ，

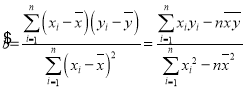    参考数据：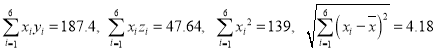

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在底面为菱形的四棱柱中，平面.

    （1）证明：平面；

    （2）求二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数（其中，m，n为常数）

    （1）当时，对有恒成立，求实数n的取值范围；

    （2）若曲线在处的切线方程为，函数的零点为，求所有满足的整数k的和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“斗拱”是中国古代建筑中特有的构件，从最初的承重作用，到明清时期集承重与装饰作用于一体.在立柱顶、额枋和檐檩间或构架间，从枋上加的一层层探出成弓形的承重结构叫拱拱与拱之间垫的方形木块叫斗.如图所示，是“散斗”（又名“三才升”）的三视图（三视图中的单位：分米），现计划用一块长方体的海南黄花梨木料加工成该散斗，则长方体木料的最小体积为（ ）立方分米.

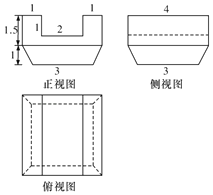
    A.40B.C.30D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知椭圆的中心为坐标原点焦点在轴上，右顶点到右焦点的距离与它到右准线的距离之比为．

    （1）求椭圆的标准方程；

    （2）若是椭圆上关于轴对称的任意两点，设，连接交椭圆于另一点．求证：直线过定点并求出点的坐标；

    （3）在（2）的条件下，过点的直线交椭圆于两点，求的取值范围．

    查看答案和解析>>

    同步练习册答案