
 有一机械传输装置(如图)将动轮⊙O的直径为2m,已知OA=2cm,OB=3cm,M、N是切点,OA∥BN,求物品从A点传输到B点的路程.
有一机械传输装置(如图)将动轮⊙O的直径为2m,已知OA=2cm,OB=3cm,M、N是切点,OA∥BN,求物品从A点传输到B点的路程. 分析 连接OM,ON,则OM⊥AM,ON⊥BN,求出AM,BN,$\widehat{MN}$,即可求物品从A点传输到B点的路程.
解答 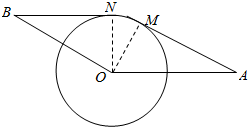 解:连接OM,ON,则OM⊥AM,ON⊥BN,
解:连接OM,ON,则OM⊥AM,ON⊥BN,
∴AM=$\sqrt{4-1}$=$\sqrt{3}$,BN=$\sqrt{9-1}$=2$\sqrt{2}$,∠AOM=60°,
∵OA∥BN,
∴∠MON=30°=$\frac{π}{6}$,
∴$\widehat{MN}$=$\frac{π}{6}$,
∴物品从A点传输到B点的路程为$\sqrt{3}$+2$\sqrt{2}$+$\frac{π}{6}$.
点评 本题考查直线与圆的位置关系,考查学生的计算能力,属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{5π}{12}$个单位 | B. | 向右平移$\frac{5π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x$+\frac{2}{x}$ | B. | y=2x+4•2-x | ||
| C. | y=$\frac{2({x}^{2}+5)}{\sqrt{{x}^{2}+4}}$ | D. | y=$\frac{4}{sinx}+sinx(0<x<4)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
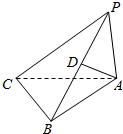 如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图所示的三棱锥P-ABC中,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,PA⊥平面ABC,则异面直线PC,AD所成角的余弦值为$\frac{\sqrt{30}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com