
(本小题满分14分)已知函数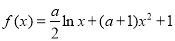 .
.
(Ⅰ)当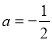 时,求
时,求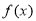 在区间
在区间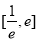 上的最小值;
上的最小值;
(Ⅱ)讨论函数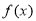 的单调性;
的单调性;
(Ⅲ)当 时,有
时,有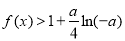 恒成立,求
恒成立,求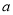 的取值范围.
的取值范围.
(Ⅰ)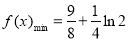 ;(Ⅱ)当
;(Ⅱ)当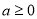 时,
时,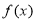 在
在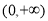 单调递增;当
单调递增;当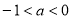 时,
时,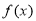 在
在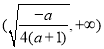 单调递增,在
单调递增,在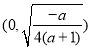 上单调递减;当
上单调递减;当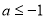 时,
时,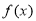 在
在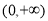 单调递减 .
单调递减 .
(Ⅲ)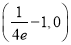 .
.
【解析】
试题分析: (Ⅰ)当 时,
时, ,对函数
,对函数 求导数,可知
求导数,可知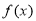 在区间
在区间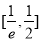 上单调递减,在区间
上单调递减,在区间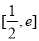 上单调递增,则
上单调递增,则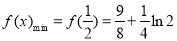 ;(Ⅱ)对函数
;(Ⅱ)对函数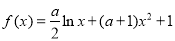 求导数得,
求导数得,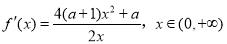 ,要分
,要分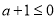 、
、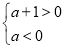 和
和
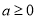 三种情况讨论,易得当
三种情况讨论,易得当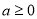 时,
时,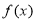 在
在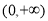 单调递增; 当
单调递增; 当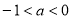 时,
时,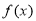 在
在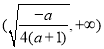 单调递增,在
单调递增,在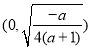 上单调递减; 当
上单调递减; 当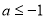 时,
时,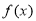 在
在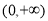 单调递减;
单调递减;
(Ⅲ)由(Ⅱ)知,当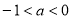 时,
时,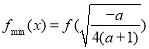 ,由题知
,由题知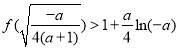 ,化简得
,化简得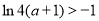 ,解得
,解得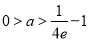 .
.
试题解析:(Ⅰ)当 时,
时, ,
,
∴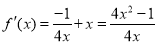 ;
;
∵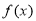 的定义域为
的定义域为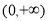 ,∴由
,∴由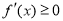 得
得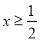 ,由
,由 得
得 .........2分
.........2分
∴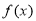 在区间
在区间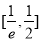 上单调递减,在区间
上单调递减,在区间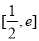 上单调递增,
上单调递增,
∴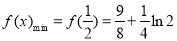 . .............4分
. .............4分
(Ⅱ)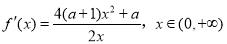 .
.
①当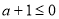 ,即
,即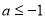 时,
时,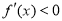 ,∴
,∴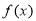 在
在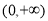 单调递减; 5分
单调递减; 5分
②当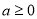 时,
时,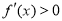 ,
,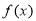 在
在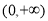 单调递增; 6分
单调递增; 6分
③当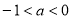 时,由
时,由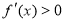 得
得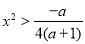 ,∴
,∴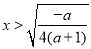 或
或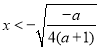 (舍去)
(舍去)
∴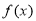 在
在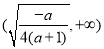 单调递增,在
单调递增,在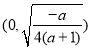 上单调递减; 8分
上单调递减; 8分
综上,当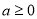 时,
时,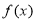 在
在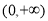 单调递增;
单调递增;
当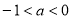 时,
时,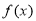 在
在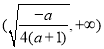 单调递增,在
单调递增,在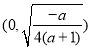 上单调递减.
上单调递减.
当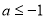 时,
时,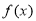 在
在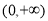 单调递减; 9分
单调递减; 9分
(Ⅲ)由(Ⅱ)知,当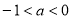 时,
时,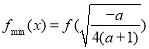 ,
,
即原不等式等价于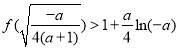 , 11分
, 11分
即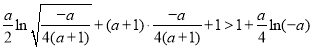 ,整理得
,整理得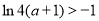
∴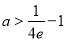 13分
13分
又∵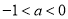 ,∴
,∴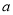 的取值范围为
的取值范围为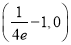 . 14分
. 14分
考点:①利用导数求最值;②利用导数讨论函数的单调性;③利用导数求参数范围.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:2014-2015学年安徽省江淮名校高三第二次联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50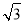 米,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路OE、EF和OF,考虑到学校整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且OE⊥OF,如图所示.
米,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路OE、EF和OF,考虑到学校整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且OE⊥OF,如图所示.
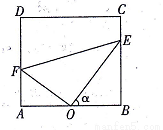
(1)设∠BOE=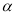 ,试将△OEF的周长L表示成
,试将△OEF的周长L表示成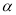 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
查看答案和解析>>
科目:高中数学 来源:2015届豫晋冀高三第二次调研考试理科数学试卷(解析版) 题型:选择题
已知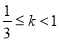 ,函数
,函数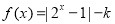 的零点分别为
的零点分别为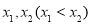 ,函数
,函数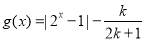 的零点分别为
的零点分别为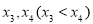 ,则
,则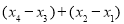 的最小值为( )
的最小值为( )
A.1 B.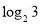 C.
C.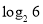 D.3
D.3
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省文登市高三上学期第一次考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在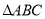 中,内角
中,内角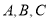 所对的边分别为
所对的边分别为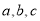 ,已知
,已知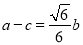 ,
,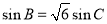 .
.
(Ⅰ)求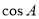 的值;
的值;
(Ⅱ)求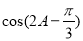 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com