
| 3 |
| 3 |
| 5 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
x03-3x0+
| ||
| x0-1 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
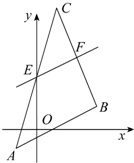 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
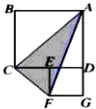 如图,点E在正方形ABCD边CD上,四边形DEFG也是正方形,已知AB=a,DE=b(a,b为常数,且a>b>0),则△ACF的面积( )
如图,点E在正方形ABCD边CD上,四边形DEFG也是正方形,已知AB=a,DE=b(a,b为常数,且a>b>0),则△ACF的面积( )| A、只与a的大小有关 |
| B、只与b的大小有关 |
| C、只与CE的大小有关 |
| D、无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 8 |
| y2 |
| 4 |
| GF |
| GP |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
| P(K2≥kc) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| Kc | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
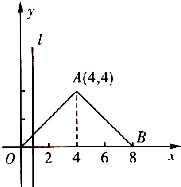 如图所示,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为(x,0).
如图所示,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为(x,0).查看答案和解析>>
科目:高中数学 来源: 题型:
| 7 |
| 9 |
| 1 |
| 2 |
| 10 |
| 27 |
| 2 |
| 3 |
| 37 |
| 48 |
| |||
| 3 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com