
【题目】为了测量山顶M的海拔高度,飞机沿水平方向在A,B两点进行测量,A,B,M在同一个铅垂面内(如图).能够测量的数据有俯角、飞机的高度和A,B两点间的距离.请你设计一个方案,包括: 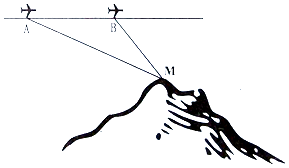
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用文字和公式写出计算山顶M海拔高度的步骤.
科目:高中数学 来源: 题型:
【题目】函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( ) 
A.(kπ﹣ ![]() ,kπ+
,kπ+ ![]() ,),k∈z
,),k∈z
B.(2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ),k∈z
),k∈z
C.(k﹣ ![]() ,k+
,k+ ![]() ),k∈z
),k∈z
D.( ![]() ,2k+
,2k+ ![]() ),k∈z
),k∈z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.
(Ⅰ)求证:平面ADEF⊥平面B1FG;
(Ⅱ)求直线AB1与平面ADEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四边形ABCD的对角线AC=10,BD=6,M、N分别为AB、CD的中点,MN=7,则异面直线AC和BD所成的角等于( )
A.30°
B.60°
C.90°
D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心为坐标原点,左焦点为F1(﹣1,0),离心率
的中心为坐标原点,左焦点为F1(﹣1,0),离心率![]() .
.
(1)求椭圆G 的标准方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,如图所示.
,如图所示.

①证明:![]() ;
;
②求四边形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中, 已知定圆
中, 已知定圆![]() ,动圆
,动圆![]() 过点
过点![]() 且与圆
且与圆![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (异于点
(异于点![]() ),若直线
),若直线![]() 分别交
分别交![]() 轴于点
轴于点![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若h(x)=g(x)﹣λf(x)+1在[﹣1,1]上是增函数,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),且直线
不重合),且直线![]() 与
与![]() 轴的交于点
轴的交于点![]() ,试问
,试问![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com