
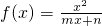 (m,n为常数),且关于x的方程f(x)=x-12有两个实数根x1=3,x2=4.
(m,n为常数),且关于x的方程f(x)=x-12有两个实数根x1=3,x2=4.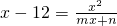 ,
,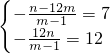 ,
,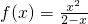 ,
,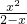 <(t+1)x-t,
<(t+1)x-t,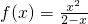 ,从而关于x的不等式:(2-x)f(x)<(t+1)x-t.化简得即(x-t)(x-1)<0(x≠2),再对t进行分类讨论,即可得出不等式的解集.
,从而关于x的不等式:(2-x)f(x)<(t+1)x-t.化简得即(x-t)(x-1)<0(x≠2),再对t进行分类讨论,即可得出不等式的解集.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:重庆市期末题 题型:解答题
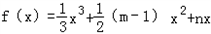 (m、n为常数).
(m、n为常数).查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市慈溪市高三(上)期中数学试卷(理科)(解析版) 题型:解答题
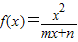 (m,n为常数),且关于x的方程f(x)=x-12有两个实数根x1=3,x2=4.
(m,n为常数),且关于x的方程f(x)=x-12有两个实数根x1=3,x2=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com