练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．命题：“?x0＞0，使2${\;}^{{x}_{0}}$（x0-a）＞1”，这个命题的否定是（　　）
    A．?x＞0，使2x（x-a）＞1B．?x＞0，使2x（x-a）≤1C．?x≤0，使2x（x-a）≤1D．?x≤0，使2x（x-a）＞1

    分析 直接利用特称命题的否定是全称命题写出结果即可．

    解答 解：因为特称命题的否定是全称命题，所以，命题的否定为?x＞0，使2x（x-a）≤1，
    故选：B．

    点评 本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=2sin（2x+$\frac{π}{6}$）+2，x∈R．求：
    （ I） 求函数f（x）的最小正周期和单调递增区间；
    （ II） 求函数f（x）在区间[-$\frac{π}{6}$，$\frac{π}{3}$]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．如图是某算法的程序框图，则程序运行后输入的结果是3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．设函数f（x）=$\frac{1}{2}$+log2$\frac{x}{1-x}$，定义Sn=f（$\frac{1}{n}$）+f（$\frac{2}{n}$）+f（$\frac{3}{n}$）+…+f（$\frac{n-1}{n}$），其中n∈N+，（n≥2）则Sn=$\frac{n}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在生产过程中，测得纤维产品的纤度（表示纤维粗细的一种量）共有100个数据，将数据分组及其频数：
    分组频数
    [1.30，1.34）4
    [1.34，1.38）25
    [1.38，1.42）30
    [1.42，1.46）29
    [1.46，1.50）10
    [1.50，1.54）2
    合计100
    （1）列出频率分布表；
    （2）画出频率分布直方图；
    （3）从频率分布直方图估计出纤度的众数、中位数和平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．如图，直角△ABC中，AB=1，BC=2，∠ABC=90°，作△ABC的内接正方形BEFB1，再作△B1FC的内接正方形B1E1F1B2，…，依次下去，所有正方形的面积依次构成数列{an}，其前n项和为$\frac{4}{5}$$[1-（\frac{4}{9}）^{n}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

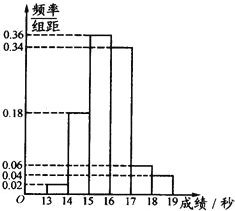    19．某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，如图是测试成绩频率分布直方图．成绩小于17秒的学生人数为（　　）
    A．45B．35C．17D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．下列函数中，既是偶函数又在（0，+∞）上单调递增的是（　　）
    A．y=exB．y=sinxC．y=cosxD．y=lnx2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．函数f（x）=$\sqrt{1-x}$+$\frac{1}{x+1}$的定义域为（-∞，-1）∪（-1，1]．

    查看答案和解析>>

    同步练习册答案