
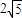 ,PA与CD所成的角的大小等于
,PA与CD所成的角的大小等于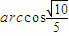 .
.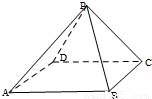
 解:(1)取AB的中点M,记正方形ABCD对角线的交点为O',连PM,PO',AC,则AC过O'.
解:(1)取AB的中点M,记正方形ABCD对角线的交点为O',连PM,PO',AC,则AC过O'.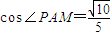 ,
,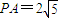 ,得
,得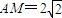 .…(4分)
.…(4分)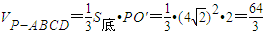
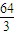 (立方单位).…(8分)
(立方单位).…(8分)

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

A.OD∥平面PBC B.OD⊥PA
C.OD⊥AC D.PA=2OD
查看答案和解析>>
科目:高中数学 来源: 题型:

A.OD∥平面PBC B.OD⊥PA
C.OD⊥AC D.PA=2OD
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一下学期第一次阶段考试理科数学 题型:填空题
在正三棱锥P—ABC中,D为PA的中点,O为△ABC的中心,给出下列四个结论:
①OD∥平面PBC; ②OD⊥PA;③OD⊥BC; ④PA=2OD.
其中正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com