
分析 (1)先根据二倍角公式两角和差的正弦公式化简,再很据正弦函数的图象和性质求出单调区间,
(2)先求出A的大小,再根据余弦定理即可求出
解答 解:(1)f(x)=2cos$\frac{ωx}{2}$sin($\frac{ωx}{2}$+$\frac{π}{6}$)-$\frac{1}{2}$=$\sqrt{3}$sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$+cos2$\frac{ωx}{2}$-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$sinωx+$\frac{1}{2}$(1+cosωx)-$\frac{1}{2}$=sin(ωx+$\frac{π}{6}$)
由相邻两条对称轴间的距离为$\frac{π}{2}$,知f(x)的最小正周期T=π,则ω=2
所以$f(x)=sin(2x+\frac{π}{6})$
令$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2},k∈Z$
得f(x)的递增区间为$[kπ-\frac{π}{3},kπ+\frac{π}{6}](k∈Z)$
(2)由$f(\frac{A}{2})-cosA=\frac{1}{2}$得$sin(A+\frac{π}{6})-cosA=\frac{1}{2}$
得$\frac{{\sqrt{3}}}{2}sinA-\frac{1}{2}cosA=\frac{1}{2}$,$sin(A-\frac{π}{6})=\frac{1}{2}$,
∵0<A<π,
∴$-\frac{π}{6}<A-\frac{π}{6}<\frac{5π}{6}$,
∴$A-\frac{π}{6}=\frac{π}{6}$,即$A=\frac{π}{3}$
又bc=1,b+c=3,
根据余弦定理可得a2=b2+c2-2bccosA=(b+c)2-3bc=6,
∴$a=\sqrt{6}$
点评 本题考查了二倍角公式两角和差的正弦公式,正弦函数的图象和性质以及余弦定理,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
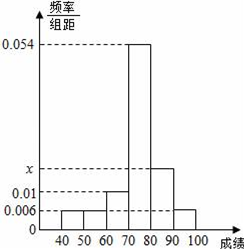 某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 11月1日 | 11月2日 | 11月3日 | 11月4日 | 11月5日 |
| 温差x(℃) | 8 | 11 | 12 | 13 | 10 |
| 发芽数y(颗) | 16 | 25 | 26 | 30 | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{21}$ | B. | $\frac{21}{13}$ | C. | $\frac{11}{13}$ | D. | $\frac{13}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com