
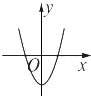
 B、
B、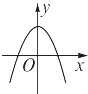 C、
C、 D、
D、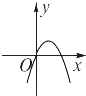
分析 求出导函数,根据导函数的二次项系数为正得到图象开口向上;利用函数解析式中有2ax,可得函数不是偶函数,得到函数的图象.再根据对称轴以及f′(0)=0求得a的值,可得f(x)的解析式,从而求得f(-1)的值.
解答 解:∵f′(x)=x2+2ax+(a2-1),∴导函数f′(x)的图象开口向上.
又∵a≠0,∴f(x)不是偶函数,其图象不关于y轴对称,
其图象必为第三张图.由图象特征知f′(0)=0,且对称轴为x=-a>0,∴a=-1,f(x)=$\frac{1}{3}$•x3-x2+1.
故f(-1)=-$\frac{1}{3}$-1+1=-$\frac{1}{3}$,
故答案为:-1.
点评 本题考查导函数的运算法则、二次函数的图象与二次函数系数的关系:开口方向与二次项系数的符号有关、对称轴公式,属于中档题.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
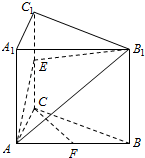 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com