
 2016��Ԭ¡ƽ�ij����ӽ�ˮ���ٴ�Ķ���������¼��Ϊ�˲���ˮ�����������ר��ѡȡ�˼ס�������أ�������������������ȡ10��ˮ���������������ǵĸ߶ȣ���õĸ߶����ݵľ�Ҷͼ��ͼ��ʾ��
2016��Ԭ¡ƽ�ij����ӽ�ˮ���ٴ�Ķ���������¼��Ϊ�˲���ˮ�����������ר��ѡȡ�˼ס�������أ�������������������ȡ10��ˮ���������������ǵĸ߶ȣ���õĸ߶����ݵľ�Ҷͼ��ͼ��ʾ������ ��1���ɾ�Ҷͼ��֪���߶ȼ�����122cm��139cm֮�䣬�Ҹ߶ȼ�����130cm��141cm֮�䣬�Ӷ���ƽ���߶ȸ��ڼף�
��2�����ݾ�Ҷͼ��������������������������ߵ�ƽ�������ɴ�����������������߷��
��3����߶�Ϊ136cm�����������е��¼�ΪA�������оٷ�������ҵ�10��ˮ�������г�������߶Ȳ�����133cm�������������ɴ�������߶�Ϊ136cm�����������еĸ��ʣ�
��� �⣺��1���ɾ�Ҷͼ��֪���߶ȼ�����122cm��139cm֮�䣬
���Ҹ߶ȼ�����130cm��141cm֮�䣬
�����ƽ���߶ȸ��ڼף�
��2�����ݾ�Ҷͼ���������ݵõ���
$\overline{x_1}=\frac{142+130+131+139+139+122+123+128+128+118}{10}=130$��
$\overline{x_2}=\frac{119+122+125+128+130+133+136+138+139+141}{10}=131.1$��$S_��^2=\frac{1}{10}[{{{��{130-142}��}^2}+{{��{130-130}��}^2}+{{��{130-131}��}^2}+{{��{130-139}��}^2}+{{��{130-139}��}^2}+{{��{130-122}��}^2}}\right.$+��130-123��2+��130-128��2+��130-128��+��130-118��2]=57.2��
$S_��^2=\frac{1}{10}[{{{��{131.1-141}��}^2}}\right.+{��{131.1-139}��^2}+{��{131.1-138}��^2}+{��{131.1-136}��^2}+{��{131.1-133}��^2}+{��{131.1-130}��^2}$+��131.1-128��2+��131.1-125��2+��131.1-122��2+��131.1-119��2]=51.29��
��3����߶�Ϊ136cm�����������е��¼�ΪA��
���ҵ�10��ˮ�������г�������߶Ȳ�����133cm�������У�
��133��136������133��138������133��139������133��141������136��138����
��136��139������136��141������138��139������138��141������139��141����10�������¼���
���¼�A����4�������¼���
��߶�Ϊ136cm�����������еĸ���$P=\frac{4}{10}=\frac{2}{5}$��
���� ���⿼�龥Ҷͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���������ֻ����ռ������繺��Խ��Խ�ܵ����ǵ�������ij�о���ѧϰС���ʹ�������ֻ�����������������10λͬѧ���õ�������ȴ���羥Ҷͼ��ʾ�����������ݵ���λ����ƽ�����ֱ�Ϊa��b����a��b�Ĵ�С��ϵ��a=b��
���������ֻ����ռ������繺��Խ��Խ�ܵ����ǵ�������ij�о���ѧϰС���ʹ�������ֻ�����������������10λͬѧ���õ�������ȴ���羥Ҷͼ��ʾ�����������ݵ���λ����ƽ�����ֱ�Ϊa��b����a��b�Ĵ�С��ϵ��a=b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
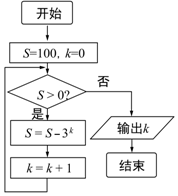
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a^3}{4}$ | B�� | $\frac{a^3}{3}$ | C�� | $\frac{a^3}{2}$ | D�� | a3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -4 | C�� | -8 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3n2 | B�� | 3n2+3n | C�� | 6n+1 | D�� | 6n-1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com