
分析 (Ⅰ)问题等价于|m+1|+|m-2|≥5,通过讨论m的范围,求出不等式的解集即可;
(Ⅱ)根据绝对值的性质证明即可.
解答 解:(Ⅰ)不等式f(1)+f(-2)≥5等价于|m+1|+|m-2|≥5,
可化为$\left\{{\begin{array}{l}{m<-1}\\{-({m+1})-({m-2})≥5}\end{array}}\right.$,解得m≤-2;
或$\left\{{\begin{array}{l}{-1≤m≤2}\\{({m+1})-({m-2})≥5}\end{array}}\right.$,无解;
或$\left\{{\begin{array}{l}{m>2}\\{({m+1})+({m-2})≥5}\end{array}}\right.$,解得m≥3;
综上不等式解集为(-∞,-2]∪[3,+∞)…(5分)
(Ⅱ)证明:当x≠0时,$|{\frac{1}{x}}|>0$,|x|>0,
$f({\frac{1}{x}})+f({-x})=|{\frac{1}{x}+m}|+|{-x+m}|≥|{({\frac{1}{x}+m})-({-x+m})}|≥|{\frac{1}{x}+x}|=|{\frac{1}{x}}|+|x|≥2$,
…(10分)
点评 本题考查了解绝对值不等式问题,考查绝对值的性质,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
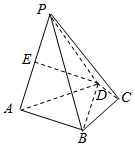 如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.
如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
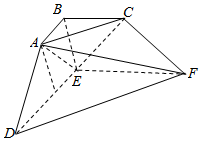 如图,三棱台ABC-DEF中,BE⊥底面DEF,AB=BE=$\frac{1}{2}$DE=1,∠ABC=90°.
如图,三棱台ABC-DEF中,BE⊥底面DEF,AB=BE=$\frac{1}{2}$DE=1,∠ABC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
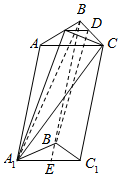 如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面ABC,△ABC为等边三角形,AB=$\frac{1}{2}$AA1=1,∠A1AB=120°,D,E分别是BC,A1C1的终点.
如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面ABC,△ABC为等边三角形,AB=$\frac{1}{2}$AA1=1,∠A1AB=120°,D,E分别是BC,A1C1的终点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$-1 | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{-\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com