
 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=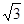 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 
A.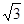 | B. | C. | D.2 |
D
解析试题分析: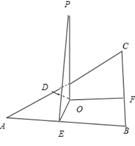
 △ABC中,∵AC=4,BC=3,
△ABC中,∵AC=4,BC=3,
∴AB=5,
过O作OE⊥AB,垂足是E,作OF⊥BC,垂足是F,作OD⊥AC,交AC于D,
∵O是△ABC的内心,
∴OE=OF=OD=r,(r是△ABC内切圆半径),
∴DC=CF=r,AD=AE=4-r,BF=BE=3-r,
∴AB=3-r+4-r=5,解得r=1,
∴OE=1,
∵PO⊥面ABC,O是△ABC的内心,PO=" 3" ,OE⊥AB,
∴PE⊥AB,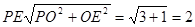 .
.
∴点P到△ABC的斜边AB的距离是2.
考点:点、线、面间的距离计算.
点评:本题考查空间中点到直线的距离的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平
面问题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:单选题
如图,在长方形ABCD中,AB=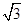 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( ) 

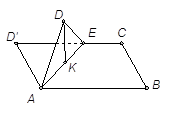
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知平面 ,直线
,直线 ,直线
,直线 ,有下面四个命题:
,有下面四个命题:
(1)  ∥
∥

 (2)
(2) 
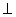


 ∥
∥
(3)  ∥
∥


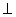
 (4)
(4) 

 ∥
∥
其中正确的是( )
| A.(1)与(2) | B.(3)与(4) | C.(1)与(3) | D.(2)与(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若a,b是两条直线,α是一个平面,则下列命题正确的是( )
| A.若a∥b,则a平行于经过b的任何平面 |
| B.若a∥α,则a与α内任何直线平行 |
| C.若a∥α,b∥α,则a∥b |
D.若a∥b,a∥α,b α,则b∥α α,则b∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知四面体OABC中,OA、OB、OC两两相互垂直, ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
A.①② B.②③ C.①③ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com