
已知四面体OABC中,OA、OB、OC两两相互垂直, ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
A.①② B.②③ C.①③ D.③④
D
解析试题分析: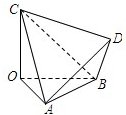
对于①,∵四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,∴AC=BC=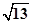 ,AB=2
,AB=2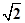 ,当四棱锥CABD与四面体OABC一样时,即取CD=3,AD=BD=2,四面体ABCD的三条棱DA、DB、DC两两垂直,此时点D,使四面体ABCD有三个面是直角三角形,故①不正确;对于②,由①知AC=BC=
,当四棱锥CABD与四面体OABC一样时,即取CD=3,AD=BD=2,四面体ABCD的三条棱DA、DB、DC两两垂直,此时点D,使四面体ABCD有三个面是直角三角形,故①不正确;对于②,由①知AC=BC=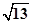 ,AB=2
,AB=2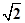 ,使AB=AD=BD,此时存在点D,CD=
,使AB=AD=BD,此时存在点D,CD=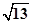 ,使四面体C-ABD是正三棱锥,故②不正确;对于③,取CD=AB,AD=BD,此时CD垂直面ABD,即存在点D,使CD与AB垂直并且相等,故③正确;对于④,先找到四面体OABC的内接球的球心P,使半径为r,只需PD=r即可,∴存在无数个点D,使点O在四面体ABCD的外接球面上,故④正确,故正确的命题有③④,故选D.
,使四面体C-ABD是正三棱锥,故②不正确;对于③,取CD=AB,AD=BD,此时CD垂直面ABD,即存在点D,使CD与AB垂直并且相等,故③正确;对于④,先找到四面体OABC的内接球的球心P,使半径为r,只需PD=r即可,∴存在无数个点D,使点O在四面体ABCD的外接球面上,故④正确,故正确的命题有③④,故选D.
考点:本题考查了空间中的线面关系
点评:本题考查棱锥的结构特征,同时考查了空间想象能力,转化与划归的思想,以及构造法的运用,属于中档题


科目:高中数学 来源: 题型:单选题
在正方体ABCD—A1B1C1D1中,M、N、P、Q分别是棱AB、BC、CD、CC1的中点,直线MN与PQ所成的度数是 ( )
A.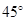 B.
B.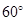 C.
C.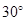 D.
D.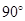
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知m,n是两条不重合的直线, 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
①若m
 ,m
,m
 ,则
,则 ∥
∥ ; ②若
; ②若

 ,
,

 则
则 ∥
∥
③若m// ,n //
,n // ,m//n 则
,m//n 则 //
// ④若m
④若m
 ,m//
,m// ,则
,则


其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列结论中正确的是( )
| A.平行于平面内两条直线的平面,一定平行于这个平面 |
| B.一条直线平行于一个平面内的无数条直线,则这条直线与该平面平行 |
| C.两个平面分别与第三个平面相交,若交线平行则两平面平行 |
| D.在两个平行平面中,一平面内的一条直线必平行于另一个平面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com