
分析 将arcsinx看成整体,设为t,转化为关于t的二次函数,再用配方法求出二次函数的最值以及对应的x的值.
解答 解:设t=arcsinx,t∈[-$\frac{π}{2}$,$\frac{π}{2}$],
则y=t2+t-1=(t+$\frac{1}{2}$)2-$\frac{5}{4}$,
所以当t=$\frac{π}{2}$时,ymax=$\frac{{π}^{2}}{4}$+$\frac{π}{2}$-1,此时x=1;
当t=-$\frac{1}{2}$时,ymin=-$\frac{5}{4}$,此时x=-sin$\frac{1}{2}$.
点评 本题考查了反三角函数的运用、二次函数最大值的求法,二次函数的最大(小)值问题,是基础题目.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 存在平面α,使得a?α且b⊥α | |
| B. | 存在平面β,使得b?β 且a∥β | |
| C. | 若点A,B分别在直线a,b上,且满足AB⊥b,则一定有AB⊥a | |
| D. | 过空间某点不一定存在与直线a,b都平行的平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
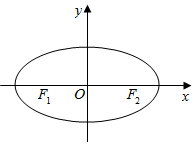 已知F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且右焦点F2的坐标为(1,0),点P(1,$\frac{\sqrt{2}}{2}$)在椭圆C上,O为坐标原点.
已知F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且右焦点F2的坐标为(1,0),点P(1,$\frac{\sqrt{2}}{2}$)在椭圆C上,O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com