
分析 (1)推导出点Q的轨迹是以点C,F为焦点,焦距为$2\sqrt{3}$,长轴为4的椭圆,由此能求出点Q的轨迹方程.
(2)①设l1的方程为y=k(x-2),联立$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{y=k({x-2})}\end{array}}\right.$,得(1+4k2)x2-16k2x+16k2-4=0,推导出$M({\frac{{8{k^2}-2}}{{1+4{k^2}}},\frac{-4k}{{1+4{k^2}}}})$,由l1,l2倾斜角互补,知l2的方程为y=-kx+1,联立$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{y=-kx+1}\end{array}}\right.$,得(1+4k2)x2-8kx=0,推导出$N({\frac{8k}{{1+4{k^2}}},\frac{{1-4{k^2}}}{{1+4{k^2}}}})$,由此能求出直线MN的斜率.
②设直线MN的方程为$y=\frac{1}{2}x+b$,联立$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{y=\frac{1}{2}x+b}\end{array}}\right.$,得x2+2bx+2b2-2=0,由此利用根的判别式、韦达定理、弦长公式、点到直线距离公式,结合已知条件能求出S的取值范围.
解答 解:(1)由题意$|{CP}|=|{QC}|+|{QP}|=|{QC}|+|{QF}|=4>|{CF}|=2\sqrt{3}$.
∴点Q的轨迹是以点C,F为焦点,焦距为$2\sqrt{3}$,长轴为4的椭圆,
所以$a=2,c=\sqrt{3},b=1$,
所以点Q的轨迹方程是$\frac{x^2}{4}+{y^2}=1$.
(2)①设l1的方程为y=k(x-2),
联立方程$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{y=k({x-2})}\end{array}}\right.$,得(1+4k2)x2-16k2x+16k2-4=0,
设l1与椭圆除A(2,0)外的另一个交点M(x1,y1),
则$2{x_1}=\frac{{16{k^2}-4}}{{1+4{k^2}}}$,${x_1}=\frac{{8{k^2}-2}}{{1+4{k^2}}}$,
代入l1的方程得${y_1}=\frac{-4k}{{1+4{k^2}}}$,∴$M({\frac{{8{k^2}-2}}{{1+4{k^2}}},\frac{-4k}{{1+4{k^2}}}})$,
∵l1,l2倾斜角互补,∴l2的方程为y=-kx+1,
联立方程组$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{y=-kx+1}\end{array}}\right.$,得(1+4k2)x2-8kx=0,
设l2与椭圆除B(0,1)外的另一个交点N(x2,y2),
则${x_2}+0=\frac{8k}{{1+4{k^2}}}$,${x_2}=\frac{8k}{{1+4{k^2}}}$,
代入l2的方程得${y_2}=\frac{{1-4{k^2}}}{{1+4{k^2}}}$,∴$N({\frac{8k}{{1+4{k^2}}},\frac{{1-4{k^2}}}{{1+4{k^2}}}})$,
∴直线MN的斜率为${k_{MN}}=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{1}{2}$.
②设直线MN的方程为$y=\frac{1}{2}x+b$,
联立方程$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{y=\frac{1}{2}x+b}\end{array}}\right.$,得x2+2bx+2b2-2=0,
由△=(2b)2-4×(2b2-2)=8-4b2>0,得$-\sqrt{2}<b<\sqrt{2}$,
设M(x1,y1),N(x2,y2),则${x_1}+{x_2}=-2b,{x_1}{x_2}=2{b^2}-2$,
∴$|{MN}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\frac{{\sqrt{5}}}{2}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=\sqrt{10-5{b^2}}$.
设d1,d2分别为点A,B到直线MN的距离,则${d_1}=\frac{{2|{1+b}|}}{{\sqrt{5}}},{d_2}=\frac{{2|{1-b}|}}{{\sqrt{5}}}$,
$S={S_{△AMN}}+{S_{△BMN}}=\frac{1}{2}|{MN}|({{d_1}+{d_2}})$═$({|{1+b}|+|{-1+b}|})\sqrt{2-{b^2}}$,
当$1<b<\sqrt{2}$时,S=$2b\sqrt{2-{b^2}}=2\sqrt{2{b^2}-{b^4}}∈({0,2})$,
当-1≤b≤1时,S=$2\sqrt{2-{b^2}}∈[{2,2\sqrt{2}}]$,
当$-\sqrt{2}<b<-1$时,S=$-2b\sqrt{2-{b^2}}=2\sqrt{2{b^2}-{b^4}}∈({0,2})$,
∴S的取值范围为$({0,2\sqrt{2}}]$.
点评 本题考查点的轨迹方程、椭圆、直线方程、根的判别式、韦达定理、弦长公式、点到直线距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | 4 | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{22}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{7}{3}$ | D. | -$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1+\sqrt{5}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
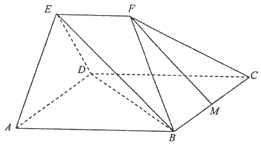 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com